Array     C++     Dynamic Programming     Hard     Memoization    

Problem Statement:

You want to schedule a list of jobs in d days. Jobs are dependent (i.e To work on the ith job, you have to finish all the jobs j where 0 <= j < i).

You have to finish at least one task every day. The difficulty of a job schedule is the sum of difficulties of each day of the d days. The difficulty of a day is the maximum difficulty of a job done on that day.

You are given an integer array jobDifficulty and an integer d. The difficulty of the ith job is jobDifficulty[i].

Return the minimum difficulty of a job schedule. If you cannot find a schedule for the jobs return -1.

 

Example 1:

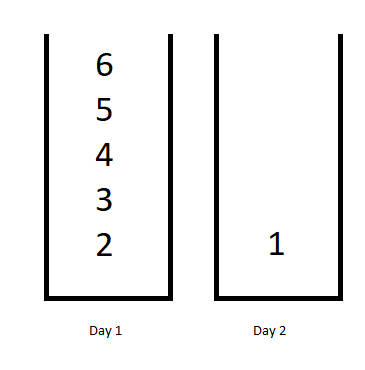
Input: jobDifficulty = [6,5,4,3,2,1], d = 2
Output: 7
Explanation: First day you can finish the first 5 jobs, total difficulty = 6.
Second day you can finish the last job, total difficulty = 1.
The difficulty of the schedule = 6 + 1 = 7

Example 2:

Input: jobDifficulty = [9,9,9], d = 4
Output: -1
Explanation: If you finish a job per day you will still have a free day. you cannot find a schedule for the given jobs.

Example 3:

Input: jobDifficulty = [1,1,1], d = 3
Output: 3
Explanation: The schedule is one job per day. total difficulty will be 3.

 

Constraints:

  • 1 <= jobDifficulty.length <= 300
  • 0 <= jobDifficulty[i] <= 1000
  • 1 <= d <= 10

Solution:

From reading the question, it is quite clear that it is a DP problem which leads us to the next problem: What is the recurrence relation?

We can see that in addition to d ie the number of cuts, we also need to consider how far we have already come in the array, ie pos. Let us call our recursive function as f(d,pos). Then the final answer can be written as f(d,0).

Say we are at position pos and we need to apply a cut to the right of any index at or after pos. Let us call this cut index as i. Then the difficulty of current day is max(jobDifficulty[pos:i]) and the remaining difficulty rem is f(d-1,i+1) because we have to make d-1 cuts in the subarray starting from i+1. So the total difficulty becomes max(jobDifficulty[pos:i]) + f(d-1,i+1). We have to minimize this for all valid values of cut indexes i and this minimized value is actually our answer for f(d,pos). Mathematically, we can write this as:

\[F(d,pos) = \min(G(d,pos,i)), i \in [pos,\vert A \vert -d]\] \[G(d,pos,i) = \max(A_{pos,..,i}) + F(d-1,i+1)\]

The limits of i in first equation comes because we need to place d-1 cuts in the remaining array and for that we need to have at least d remaining length.

Base cases:

  • $d > \vert A \vert $ then there is no way to design the schedule. Hence return -1.
  • $d == 1$ Then we have to do all jobs in same day, so we return the maximum from pos.
 
class Solution {
    vector<vector<int>> memo = vector<vector<int>>(20, vector<int>(2000,-1));
public:
    int minDifficulty(vector<int>& jobDifficulty, int d, int pos=0) 
    {
        if (d > jobDifficulty.size()) return -1;
        if(memo[d][pos]!=-1) return memo[d][pos];
        if (d==1) return *max_element(jobDifficulty.begin()+pos,jobDifficulty.end());
        int curMax = INT_MIN, res=INT_MAX;
        for(int i=pos; i<=jobDifficulty.size()-d; i++) 
        {
            int rem = minDifficulty(jobDifficulty, d-1, i+1);
            curMax = max(curMax, jobDifficulty[i]);
            res = min(res, curMax+rem);
        }
        return memo[d][pos] = res;
    }
};

$ TC: O(n^2d) , SC: O(nd)$