Problem Statement:

Given the head of a linked list, reverse the nodes of the list k at a time, and return the modified list.

k is a positive integer and is less than or equal to the length of the linked list. If the number of nodes is not a multiple of k then left-out nodes, in the end, should remain as it is.

You may not alter the values in the list's nodes, only nodes themselves may be changed.

Example 1:

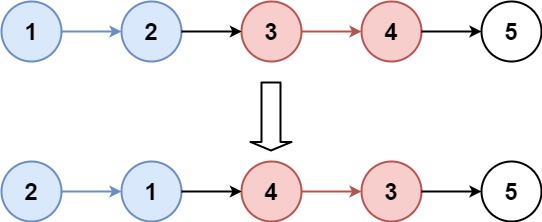
Input: head = [1,2,3,4,5], k = 2
Output: [2,1,4,3,5]

Example 2:

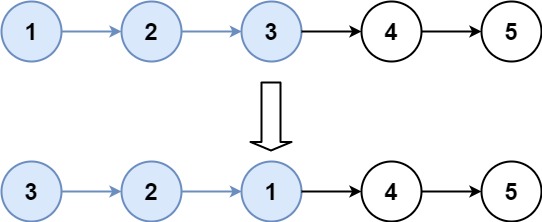
Input: head = [1,2,3,4,5], k = 3
Output: [3,2,1,4,5]

Constraints:

The number of nodes in the list is n.
1 <= k <= n <= 5000
0 <= Node.val <= 1000

Follow-up: Can you solve the problem in O(1) extra memory space?

Solution:

Here is the code to reverse linked list:

 
ListNode* reverse(ListNode* head) 
{
	ListNode *curr=head, *prev=NULL, *upcoming;
	while (curr)
	{
		upcoming = curr->next;
		curr->next = prev;
		prev = curr;
		curr = upcoming;
	}
	return prev;
}

Code is pretty much self-explanatory. Here is an example:

 
head=1,2,3,NULL

After 1st iteration:

 
head=1,NULL
prev=1,NULL
curr=2,3,NULL

After 2nd iteration:

 
head=1,NULL
prev=2,1,NULL
curr=3,NULL

After 3rd iteration

 
head=1,NULL
prev=3,2,1,NULL
curr=NULL

Now it stops.

Now to solve our question and inspired from above logic, we replace constraint in while(curr) so that it stops when we have done k iterations. For example

 
head=1,2,3,4,5,NULL
k=2

When while loop stops we will have

 
head=1,NULL
prev=2,1,NULL
curr=3,4,5,NULL

Now we need to check if the remaining part of LL 3,4,5,NULL requires reversal or not. If it does, then we add the reverse part of the remaining LL to head which is still at 1. If not we add the remaining LL without reversal to head. Finally return prev.

C++ code:

 
class Solution {
public:
    bool countK(ListNode *node, int k)
    {
        int i=0;
        while (node && i<k)
        {
            node = node->next;
            i++;
        }
        return (i==k);
    }
    ListNode* reverseKGroup(ListNode* head, int k) 
    {
        ListNode *curr=head, *prev=NULL, *upcoming;
        int i=0;
        while (i<k)
        {
            upcoming = curr->next;
            curr->next = prev;
            prev = curr;
            curr = upcoming;
            i++;
        }
        if (curr && countK(curr, k))
            head->next = reverseKGroup(curr, k);
        else
            head->next = curr;
        return prev;
    }
};