Array     C++     Graph     Hard     Java     Sort     Sorting     Union Find    

Problem Statement:

An undirected graph of n nodes is defined by edgeList, where edgeList[i] = [ui, vi, disi] denotes an edge between nodes ui and vi with distance disi. Note that there may be multiple edges between two nodes.

Given an array queries, where queries[j] = [pj, qj, limitj], your task is to determine for each queries[j] whether there is a path between pj and qj such that each edge on the path has a distance strictly less than limitj .

Return a boolean array answer, where answer.length == queries.length and the jth value of answer is true if there is a path for queries[j] is true, and false otherwise.

 

Example 1:

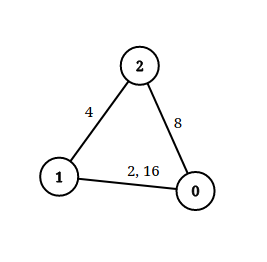
Input: n = 3, edgeList = [[0,1,2],[1,2,4],[2,0,8],[1,0,16]], queries = [[0,1,2],[0,2,5]]
Output: [false,true]
Explanation: The above figure shows the given graph. Note that there are two overlapping edges between 0 and 1 with distances 2 and 16.
For the first query, between 0 and 1 there is no path where each distance is less than 2, thus we return false for this query.
For the second query, there is a path (0 -> 1 -> 2) of two edges with distances less than 5, thus we return true for this query.

Example 2:

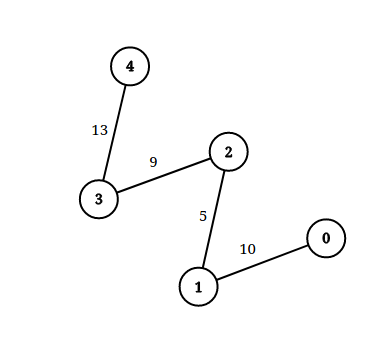
Input: n = 5, edgeList = [[0,1,10],[1,2,5],[2,3,9],[3,4,13]], queries = [[0,4,14],[1,4,13]]
Output: [true,false]
Exaplanation: The above figure shows the given graph.

 

Constraints:

  • 2 <= n <= 105
  • 1 <= edgeList.length, queries.length <= 105
  • edgeList[i].length == 3
  • queries[j].length == 3
  • 0 <= ui, vi, pj, qj <= n - 1
  • ui != vi
  • pj != qj
  • 1 <= disi, limitj <= 109
  • There may be multiple edges between two nodes.

Solution:

The idea is to pre-sort the edges by their lengths and queries by their limits. Then, for any given query we will have some set of edges. Notice that as we traverse query after query, this set of edges can only get larger as limit for edge length increases. For each query, we use the Union-Find data structure at that point to find whether the nodes in query are connected or not with the valid edges at that point. This gives us the answer for that query.

C++ code:

 
class UnionFind {
public:
    UnionFind(int sz) : roots(sz), ranks(sz) 
    {
        for (int i = 0; i < sz; ++i) {roots[i] = i; ranks[i]=0;}
    }
    int find(int x) 
    {
        if (x==roots[x]) return x;
        return roots[x] = find(roots[x]);
    }
    void unionSet(int x, int y) 
    {
        int rootX = find(x);
        int rootY = find(y);
        if (rootX == rootY) return;
        if(ranks[rootX]==ranks[rootY]) ranks[rootX]++;
        else if (ranks[rootX]<ranks[rootY]) swap(rootY,rootX);
        roots[rootY] = rootX;
    }
    bool isConnected(int x, int y)
    {
      return (find(x)==find(y));
    }
private:
    vector<int> roots;
    vector<int> ranks;
};



class Solution {
public:
    vector<bool> distanceLimitedPathsExist(int n, vector<vector<int>>& edgeList, vector<vector<int>>& queries) 
    {
        auto cmp = [](const vector<int>&veca, const vector<int>&vecb){return veca[2]<vecb[2];};
        sort(edgeList.begin(), edgeList.end(), cmp);
        for(int i=0; i<queries.size(); i++) queries[i].push_back(i);
        sort(queries.begin(), queries.end(), cmp);

        UnionFind uf = UnionFind(n);
        vector<bool>res(queries.size());
        int edgeIdx = 0;
        for (auto &query: queries)
        {
            int p=query[0], q=query[1], limit=query[2], qIdx=query[3];
            while (edgeIdx<edgeList.size()) 
            {
                int u=edgeList[edgeIdx][0], v=edgeList[edgeIdx][1], dis=edgeList[edgeIdx][2];
                if (dis>=limit) break;
                uf.unionSet(u, v);
                edgeIdx++;
            }
            res[qIdx] = uf.isConnected(p,q);
        }
        return res;
    }
};

Java code:

 
class UnionFind
{
    int[] roots;
    int[] ranks;
    public UnionFind(int sz)
    {
        roots = new int[sz];
        ranks = new int[sz];
        for(int i=0; i<sz; i++){roots[i]=i; ranks[i]=0;}
    }
    public void unionSet(int x, int y)
    {
        int rootX = find(x);
        int rootY = find(y);
        if (rootX==rootY) return;
        if (ranks[rootX]<ranks[rootY]){int temp=rootX;rootX=rootY;rootY=temp;}
        roots[rootY] = rootX;
    }
    public int find(int x)
    {
        if (x==roots[x]) return x;
        return roots[x] = find(roots[x]);
    }
    public boolean isConnected(int x, int y)
    {
        return (find(x)==find(y));
    }
}


class Solution {
    public boolean[] distanceLimitedPathsExist(int n, int[][] edgeList, int[][] queries) 
    {
        Arrays.sort(edgeList, (veca,vecb)->veca[2]-vecb[2]);
        for (int i=0; i<queries.length; i++)
        {
            int[] row = queries[i]; queries[i] = new int[4];
            for(int j=0;j<3;j++)queries[i][j]=row[j];queries[i][3]=i;
        }
        Arrays.sort(queries, (veca,vecb)->veca[2]-vecb[2]);

        UnionFind uf = new UnionFind(n);
        boolean[] res = new boolean[queries.length];
        int edgeIdx = 0;
        for (int[] query: queries)
        {
            int p=query[0], q=query[1], limit=query[2], qIdx=query[3];
            while (edgeIdx<edgeList.length) 
            {
                int u=edgeList[edgeIdx][0], v=edgeList[edgeIdx][1], dis=edgeList[edgeIdx][2];
                if (dis>=limit) break;
                uf.unionSet(u, v);
                edgeIdx++;
            }
            res[qIdx] = uf.isConnected(p,q);
        }
        return res;
    }
}