Problem Statement:

There are two types of persons:

The good person: The person who always tells the truth.
The bad person: The person who might tell the truth and might lie.

You are given a 0-indexed 2D integer array statements of size n x n that represents the statements made by n people about each other. More specifically, statements[i][j] could be one of the following:

0 which represents a statement made by person i that person j is a bad person.
1 which represents a statement made by person i that person j is a good person.
2 represents that no statement is made by person i about person j.

Additionally, no person ever makes a statement about themselves. Formally, we have that statements[i][i] = 2 for all 0 <= i < n.

Return the maximum number of people who can be good based on the statements made by the n people.

Example 1:

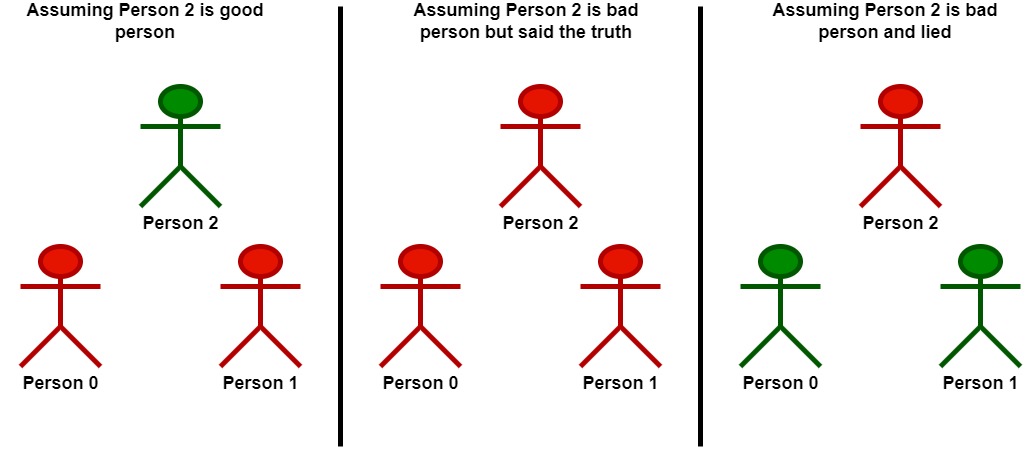
Input: statements = [[2,1,2],[1,2,2],[2,0,2]]
Output: 2
Explanation: Each person makes a single statement.
- Person 0 states that person 1 is good.
- Person 1 states that person 0 is good.
- Person 2 states that person 1 is bad.
Let's take person 2 as the key.
- Assuming that person 2 is a good person:
- Based on the statement made by person 2, person 1 is a bad person.
- Now we know for sure that person 1 is bad and person 2 is good.
- Based on the statement made by person 1, and since person 1 is bad, they could be:
- telling the truth. There will be a contradiction in this case and this assumption is invalid.
- lying. In this case, person 0 is also a bad person and lied in their statement.
- Following that person 2 is a good person, there will be only one good person in the group.
- Assuming that person 2 is a bad person:
- Based on the statement made by person 2, and since person 2 is bad, they could be:
- telling the truth. Following this scenario, person 0 and 1 are both bad as explained before.
- Following that person 2 is bad but told the truth, there will be no good persons in the group.
- lying. In this case person 1 is a good person.
- Since person 1 is a good person, person 0 is also a good person.
- Following that person 2 is bad and lied, there will be two good persons in the group.
We can see that at most 2 persons are good in the best case, so we return 2.
Note that there is more than one way to arrive at this conclusion.

Example 2:

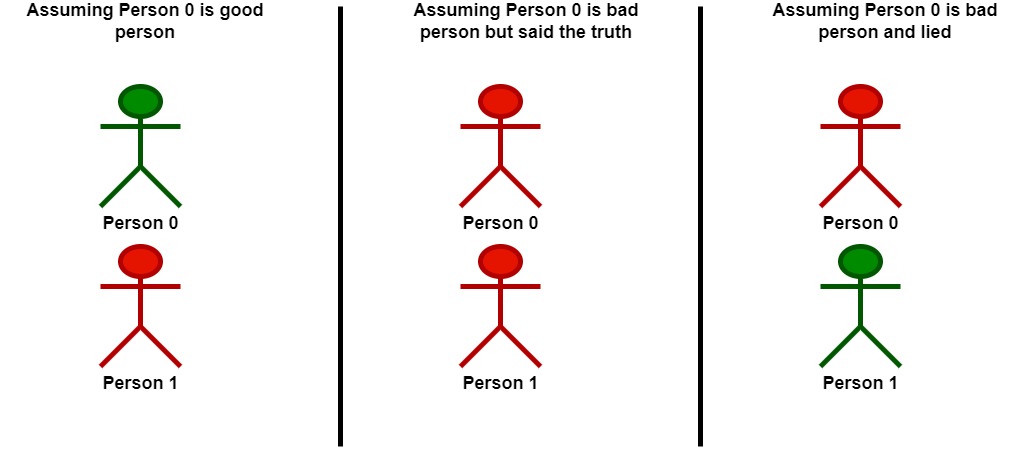
Input: statements = [[2,0],[0,2]]
Output: 1
Explanation: Each person makes a single statement.
- Person 0 states that person 1 is bad.
- Person 1 states that person 0 is bad.
Let's take person 0 as the key.
- Assuming that person 0 is a good person:
    - Based on the statement made by person 0, person 1 is a bad person and was lying.
    - Following that person 0 is a good person, there will be only one good person in the group.
- Assuming that person 0 is a bad person:
    - Based on the statement made by person 0, and since person 0 is bad, they could be:
        - telling the truth. Following this scenario, person 0 and 1 are both bad.
            - Following that person 0 is bad but told the truth, there will be no good persons in the group.
        - lying. In this case person 1 is a good person.
            - Following that person 0 is bad and lied, there will be only one good person in the group.
We can see that at most, one person is good in the best case, so we return 1.
Note that there is more than one way to arrive at this conclusion.

Constraints:

n == statements.length == statements[i].length
2 <= n <= 15
statements[i][j] is either 0, 1, or 2.
statements[i][i] == 2

Solution:

Algorithm

We have a statements matrix of size n by n made up of elements 0,1,2 where

statements[i][j]=1 means person i thinks person j is good.
statements[i][j]=0 means person i thinks person j is bad.
statements[i][j]=2 means person i doesnt comment on person j.

We also have these conditions:

Good person speaks truth always
Bad person can say truth or lie

We want to assign either 1 (for good) and 0 (for bad) to all persons in 0,1,..n-1 such that the statements matrix is feasible.

Pseudocode

Now let us write our pseudocode to validate an assignment:

 
FOR i in 0,..,n-1
	FOR j in 0,..,n-1
			IF person i is good AND person j \u2260  statement of person i on person j
				RETURN False
RETURN True

We simply need to run this for all possible assignments and if the assignment is valid we count the number of ones. At the end we return the maximum number of ones out of all valid assignments.

Bitmask

Now, to use bitmask, let us have some notation: We have 2^n ways of doing the assignment (each person can be either good or bad). Let us denote an assignment as a variable caleld number which is in the range [0,2^n-1]. If ith digit from left is 1 then in our assignment person i is assigned good and if ith digit from left is 0 then in our assignment person i is assigned bad. For example say n is 3. The we can have 0,1,2,3,4,5,6,7 as possible assignments. 0 in binary is 000 so means all bad 1 in binary is 001 so means (0,1) are bad and 2 is good 5 in binary is 101 so means (0,2) are good, 1 is bad and so on.

Now let us write some logic we are gonna use later:

How do we find if in our assignment ith person is assigned good or bad?

For exampel say our assignment is 5 ie 101. Then

5 & 4 > 0 means person 0 is assigned 1 ie good
5 & 2 == 0 means person 1 is assigned 0 ie bad
5 & 1 > 0 means person 2 is assigned 1 ie good

Basically it is just a way of iterating over the binary representation of the number.

Now that we have all the pieces let us write the code:

Time complexity: O((n^2 )* (2^n)) Space complexity: O(1)

This solution beats 80% of the solutions in terms of runtime and beats 95% of solutions in terms of memory. Please upvote if you found this helpful.