Most Frequent Subtree Sum - Plain and simple DFS

Binary Tree     C++     Depth-First Search     Hash Table     Medium     Tree    

Problem Statement:

Given the root of a binary tree, return the most frequent subtree sum. If there is a tie, return all the values with the highest frequency in any order.

The subtree sum of a node is defined as the sum of all the node values formed by the subtree rooted at that node (including the node itself).

 

Example 1:

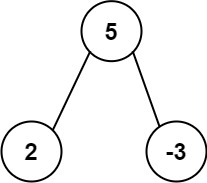
Input: root = [5,2,-3]
Output: [2,-3,4]

Example 2:

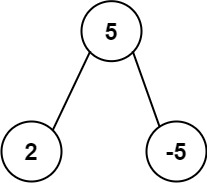
Input: root = [5,2,-5]
Output: [2]

 

Constraints:

• The number of nodes in the tree is in the range [1, 104].
• -105 <= Node.val <= 105

Solution:

Basically there are two steps to this:

• Creating a frquency map of subtree sums
• Finding the key or keys with maximum value in a frequency map.

For first part, we can modify the basic DFS to maintain subtree sums and also increment a frequency map.

For the second part, we just iterate the frequency map to get the key or keys with maximum value.

 
class Solution {
    unordered_map<int,int> H;
    int dfs(TreeNode *root)
    {
        if(!root) return 0;
        int cur = root->val + dfs(root->left) + dfs(root->right);
        H[cur]++;
        return cur;
    }
public:
    vector<int> findFrequentTreeSum(TreeNode* root) 
    {
        dfs(root);
        vector<int> res;
        int curMax = 0;
        for(auto &[k,v]: H)
        {
            if(v<curMax) continue;
            if(v==curMax){res.push_back(k); continue;}
            curMax = v;
            res.clear();
            res.push_back(k);
        }
        return res;
    }
};