Problem Statement:

You have n binary tree nodes numbered from 0 to n - 1 where node i has two children leftChild[i] and rightChild[i], return true if and only if all the given nodes form exactly one valid binary tree.

If node i has no left child then leftChild[i] will equal -1, similarly for the right child.

Note that the nodes have no values and that we only use the node numbers in this problem.

Example 1:

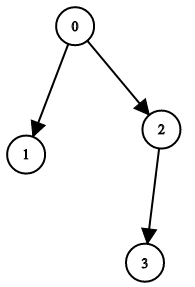
Input: n = 4, leftChild = [1,-1,3,-1], rightChild = [2,-1,-1,-1]
Output: true

Example 2:

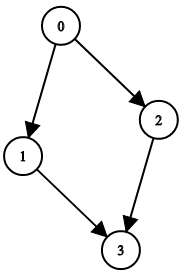
Input: n = 4, leftChild = [1,-1,3,-1], rightChild = [2,3,-1,-1]
Output: false

Example 3:

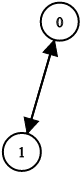
Input: n = 2, leftChild = [1,0], rightChild = [-1,-1]
Output: false

Constraints:

n == leftChild.length == rightChild.length
1 <= n <= 10⁴
-1 <= leftChild[i], rightChild[i] <= n - 1

Solution:

One way to solve this is to find root and do a DFS traversal. If there is no root or if there are more than one roots, we can return false straight-away. Further, during the DFS traversal we check that we have not seen the current node earlier. For finding the root, we can use simple logic: Root is whichever node is never seen in either of the children arrays.

I thought this much is enough but there is a case where I got WA for one case:

 
4
[1,0,3,-1]
[-1,-1,-1,-1]

On checking you will see that we will need to add one more test to check that the tree rooted at the root we found indeed contains all the nodes from 0 to n-1, so we add a test to count all nodes at the end (nodes.size()==n).

 
class Solution {
public:
    bool dfs(int root, vector<int>&lc, vector<int>&rc, unordered_set<int>&nodes)
    {
        if (root==-1) return true;
        if (nodes.count(root)) return false;
        nodes.insert(root);
        return dfs(lc[root], lc, rc, nodes) && dfs(rc[root], lc, rc, nodes);
    }
    bool validateBinaryTreeNodes(int n, vector<int>& leftChild, vector<int>& rightChild) 
    {
        unordered_set<int> childrens;
        for (int i=0; i<n; i++){childrens.insert(leftChild[i]); childrens.insert(rightChild[i]);}
        childrens.erase(-1);
        if (childrens.size()!=n-1) return false;
        int root;
        for (int i=0; i<n; i++) if (!childrens.count(i)) root = i;
        unordered_set<int> nodes;
        return dfs(root, leftChild, rightChild, nodes) && nodes.size()==n;
    }
};

An alternative solution to find root is by checking inDegree of each node. No node can have more than one inDegree and exactly one node must have zero inDegree which is the root. Again we will need to check the count of nodes.

 
class Solution {
public:
    int count(int root, vector<int>&lc, vector<int>&rc)
    {
        if (root<0) return 0;
        return 1 + count(lc[root],lc,rc) + count(rc[root],lc,rc);
    }
    bool validateBinaryTreeNodes(int n, vector<int>& leftChild, vector<int>& rightChild) 
    {
        vector<int> inDegree(n,0);
        for (int i=0;i<n;i++)
        {
            int lc = leftChild[i], rc=rightChild[i];
            if (lc>=0) if (inDegree[lc]) return false; else inDegree[lc]++;
            if (rc>=0) if (inDegree[rc]) return false; else inDegree[rc]++;
        }
        int root = -1;
        for (int i=0; i<n; i++) if (!inDegree[i]) if (root>=0) return false; else root = i;
        if (root<0) return false;
        return count(root,leftChild,rightChild)==n;
    }
};

Both the solutions give us AC and are $O(n)$ in TC as well as SC.

Hope this helps!