Binary Search Tree     Binary Tree     C++     Divide and Conquer     Linked List     Medium     Tree    

Problem Statement:

Given the head of a singly linked list where elements are sorted in ascending order, convert it to a height-balanced binary search tree.

 

Example 1:

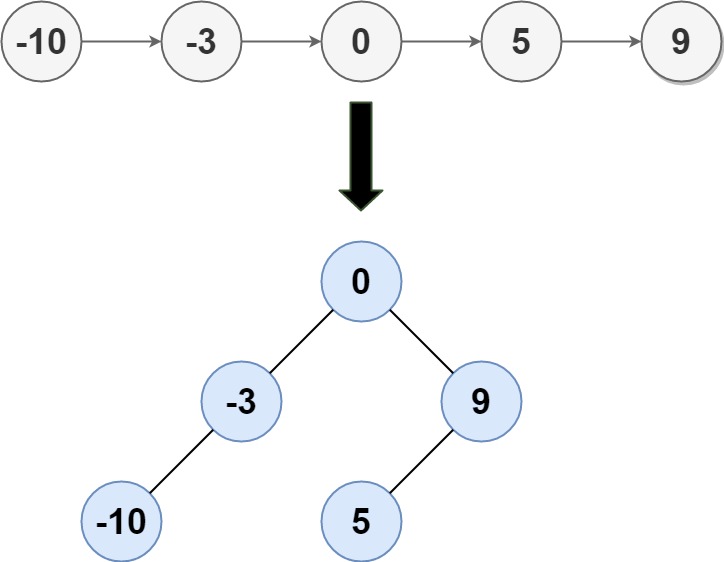
Input: head = [-10,-3,0,5,9]
Output: [0,-3,9,-10,null,5]
Explanation: One possible answer is [0,-3,9,-10,null,5], which represents the shown height balanced BST.

Example 2:

Input: head = []
Output: []

 

Constraints:

  • The number of nodes in head is in the range [0, 2 * 104].
  • -105 <= Node.val <= 105

Solution:

Intuition

The underlying thought is actually pretty simple and common in linked list problems: a tortoise and a hare; 2 pointers that walk on linked lists at 1 node per step for tortoise and 2 nodes per step for hare. When the hare reaches the end, the tortoise has reached the mid of the linked list, which is to be the root of the BST. The left subtree is to the left of this node and the right subtree is to the right, hence we can use recursion to form both subtrees. The boundary line case is when there is no node to traverse, we return null pointer in this case.

Code

 
TreeNode* sortedListToBST(ListNode* head, ListNode *end=NULL) 
{
    if (head==end) return NULL;
    ListNode *fast = head, *slow = head;
    while (fast!=end && fast->next!=end)
    {
        slow = slow->next;
        fast = fast->next->next;
    }
    TreeNode *cur = new TreeNode;
    cur->val = slow->val;
    cur->left = sortedListToBST(head, slow);
    cur->right = sortedListToBST(slow->next, end);
    return cur;
}

TC: $O(n \log n)$ SC: $O(1)$