Minimum Number of Operations to Sort a Binary Tree by Level - BFS + Min swaps to sort
Problem Statement:
You are given the root of a binary tree with unique values.
In one operation, you can choose any two nodes at the same level and swap their values.
Return the minimum number of operations needed to make the values at each level sorted in a strictly increasing order.
The level of a node is the number of edges along the path between it and the root node.
Example 1:
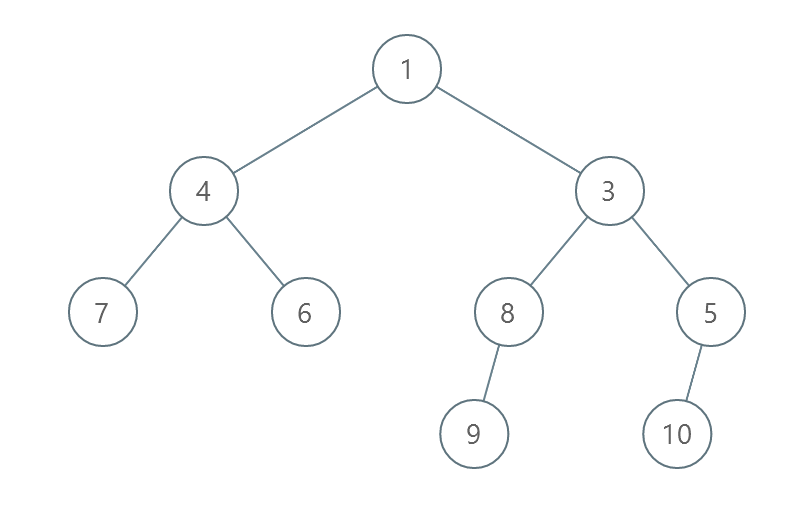
Input: root = [1,4,3,7,6,8,5,null,null,null,null,9,null,10] Output: 3 Explanation: - Swap 4 and 3. The 2nd level becomes [3,4]. - Swap 7 and 5. The 3rd level becomes [5,6,8,7]. - Swap 8 and 7. The 3rd level becomes [5,6,7,8]. We used 3 operations so return 3. It can be proven that 3 is the minimum number of operations needed.
Example 2:
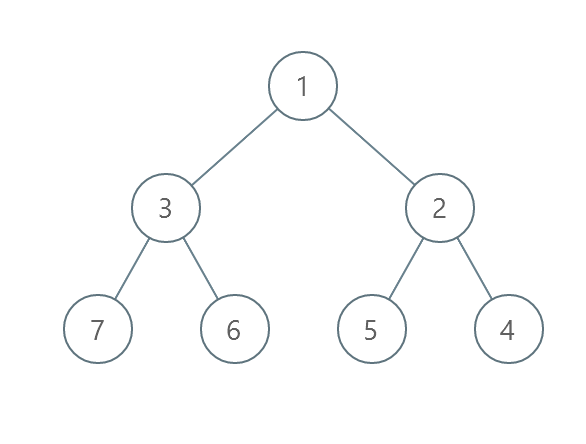
Input: root = [1,3,2,7,6,5,4] Output: 3 Explanation: - Swap 3 and 2. The 2nd level becomes [2,3]. - Swap 7 and 4. The 3rd level becomes [4,6,5,7]. - Swap 6 and 5. The 3rd level becomes [4,5,6,7]. We used 3 operations so return 3. It can be proven that 3 is the minimum number of operations needed.
Example 3:
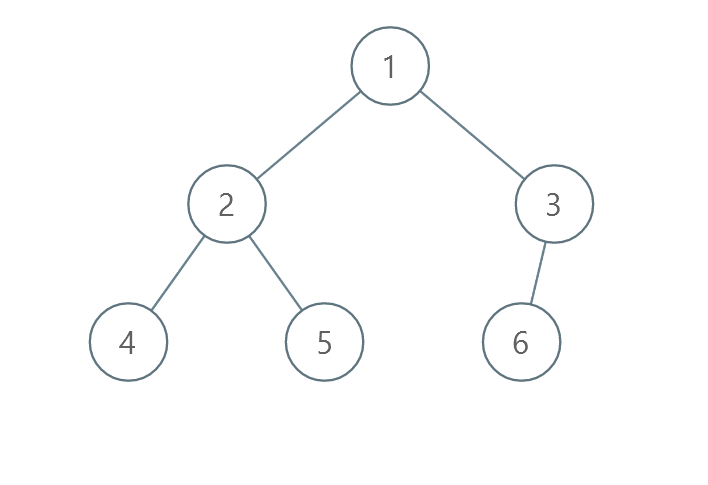
Input: root = [1,2,3,4,5,6] Output: 0 Explanation: Each level is already sorted in increasing order so return 0.
Constraints:
- The number of nodes in the tree is in the range
[1, 105]. 1 <= Node.val <= 105- All the values of the tree are unique.
Solution:
Use BFS to get nodes at each level. Then we need an algorithm to find minimum number of swaps to sort an array. I used this reference for this part. The idea is simple: Traverse through sorted version of array and try to get back original array by swapping repeatedly.
class Solution {
public:
int numSwaps(vector<int> &A)
{
int swaps = 0, n=A.size();
vector<pair<int,int>> vec;
for (int i=0; i<n; i++) vec.push_back({A[i],i});
sort(vec.begin(),vec.end());
for (int i=0; i<n; i++)
{
int value=vec[i].first, index=vec[i].second;
if (i!=index)
{
swaps++;
swap(vec[i], vec[index]);
i--;
}
}
return swaps;
}
int minimumOperations(TreeNode* root)
{
queue<TreeNode *>Q;
Q.push(root);
int ctr = 0;
while(!Q.empty())
{
vector<int> vals;
for (int i=Q.size(); i>0; i--)
{
TreeNode *u = Q.front();
Q.pop();
vals.push_back(u->val);
if (u->left) Q.push(u->left);
if (u->right) Q.push(u->right);
}
if (vals.size()<=1) continue;
ctr += numSwaps(vals);
}
return ctr;
}
};