Add One Row to Tree - Easy to understand DFS solution

Binary Tree     Breadth-First Search     Depth-First Search     Medium     Tree    

Problem Statement:

Given the root of a binary tree and two integers val and depth, add a row of nodes with value val at the given depth depth.

Note that the root node is at depth 1.

The adding rule is:

• Given the integer depth, for each not null tree node cur at the depth depth - 1, create two tree nodes with value val as cur's left subtree root and right subtree root.
• cur's original left subtree should be the left subtree of the new left subtree root.
• cur's original right subtree should be the right subtree of the new right subtree root.
• If depth == 1 that means there is no depth depth - 1 at all, then create a tree node with value val as the new root of the whole original tree, and the original tree is the new root's left subtree.

 

Example 1:

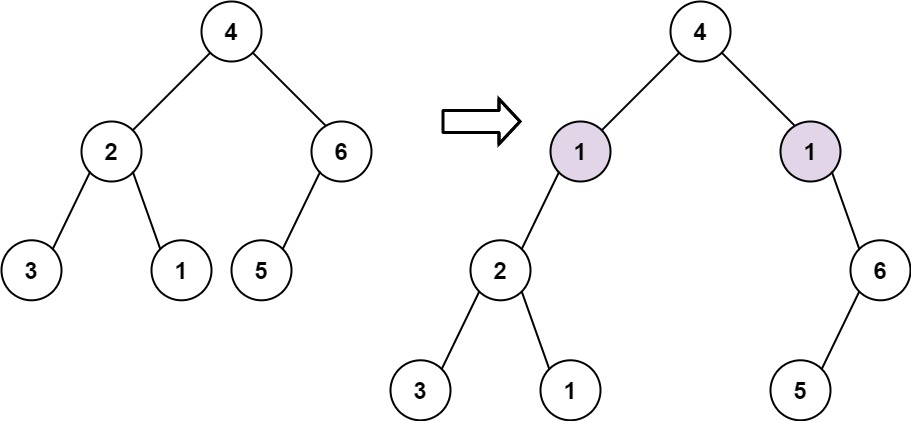
Input: root = [4,2,6,3,1,5], val = 1, depth = 2
Output: [4,1,1,2,null,null,6,3,1,5]

Example 2:

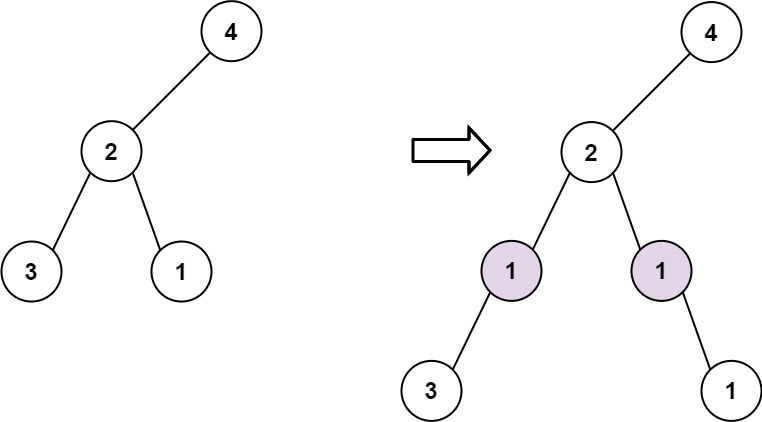
Input: root = [4,2,null,3,1], val = 1, depth = 3
Output: [4,2,null,1,1,3,null,null,1]

 

Constraints:

• The number of nodes in the tree is in the range [1, 104].
• The depth of the tree is in the range [1, 104].
• -100 <= Node.val <= 100
• -105 <= val <= 105
• 1 <= depth <= the depth of tree + 1

Solution:

This is a plain DFS problem. Logic in comments.

class Solution {
public:
    void dfs(TreeNode *root, int val, int depth, int curDepth)
    {
        if (!root) return;
		// We need to insert as per the rule at this point
        if (depth==curDepth+1)
        {
            root->left = new TreeNode(val, root->left, NULL);
            root->right = new TreeNode(val, NULL, root->right);
            return;
        }
        dfs(root->left, val, depth, curDepth+1);
        dfs(root->right, val, depth, curDepth+1);
    }
    TreeNode* addOneRow(TreeNode* root, int val, int depth) 
    {
		// Special case when we have to insert at root
        if (depth==1) return new TreeNode(val, root, NULL);
        dfs(root, val, depth, 1);
        return root;
    }
};