Parallel Courses III - Process in topological order
Problem Statement:
You are given an integer n, which indicates that there are n courses labeled from 1 to n. You are also given a 2D integer array relations where relations[j] = [prevCoursej, nextCoursej] denotes that course prevCoursej has to be completed before course nextCoursej (prerequisite relationship). Furthermore, you are given a 0-indexed integer array time where time[i] denotes how many months it takes to complete the (i+1)th course.
You must find the minimum number of months needed to complete all the courses following these rules:
- You may start taking a course at any time if the prerequisites are met.
- Any number of courses can be taken at the same time.
Return the minimum number of months needed to complete all the courses.
Note: The test cases are generated such that it is possible to complete every course (i.e., the graph is a directed acyclic graph).
Example 1:

Input: n = 3, relations = [[1,3],[2,3]], time = [3,2,5] Output: 8 Explanation: The figure above represents the given graph and the time required to complete each course. We start course 1 and course 2 simultaneously at month 0. Course 1 takes 3 months and course 2 takes 2 months to complete respectively. Thus, the earliest time we can start course 3 is at month 3, and the total time required is 3 + 5 = 8 months.
Example 2:
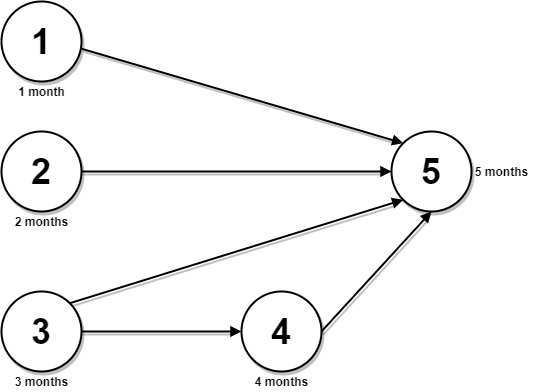
Input: n = 5, relations = [[1,5],[2,5],[3,5],[3,4],[4,5]], time = [1,2,3,4,5] Output: 12 Explanation: The figure above represents the given graph and the time required to complete each course. You can start courses 1, 2, and 3 at month 0. You can complete them after 1, 2, and 3 months respectively. Course 4 can be taken only after course 3 is completed, i.e., after 3 months. It is completed after 3 + 4 = 7 months. Course 5 can be taken only after courses 1, 2, 3, and 4 have been completed, i.e., after max(1,2,3,7) = 7 months. Thus, the minimum time needed to complete all the courses is 7 + 5 = 12 months.
Constraints:
1 <= n <= 5 * 1040 <= relations.length <= min(n * (n - 1) / 2, 5 * 104)relations[j].length == 21 <= prevCoursej, nextCoursej <= nprevCoursej != nextCoursej- All the pairs
[prevCoursej, nextCoursej]are unique. time.length == n1 <= time[i] <= 104- The given graph is a directed acyclic graph.
Solution:
First of all we need to understand Topological ordering. It is an ordering of nodes in which for every edge $u ightarrow v$, $u$ comes before $v$. The basic logic is quite easy: Maintain a queue of nodes with zero inDegree.
Here is how you get topological ordering given a graph G and an array inDegree:
queue<int>Q; vector<int> top_ord;
for(int i=0;i<n;i++) if(!inDegree[i]) Q.push(i);
while (!Q.empty())
{
int u = Q.front(); Q.pop(); top_ord.push_back(u);
for (int v: G[u]) if (!inDegree[v]--) Q.push(v);
}
Now, we modify the code such that we process the graph in this ordering and we store the minimum time a course can be finished in the array minTime. Every time we have an edge $u ightarrow v$, we do minTime[v] = max(minTime[v], minTime[u]+time[v]); which means maximum end time of prerequisite courses and current course.
class Solution
{
public:
int minimumTime(int n, vector<vector<int>>& relations, vector<int>& time)
{
vector<vector<int>> G(n);
vector<int> inDegree(n,0);
for(auto &r: relations)
{
int u=r[0]-1, v=r[1]-1;
G[u].push_back(v);
inDegree[v]++;
}
queue<int>Q;
vector<int> minTime(n,0);
for(int i=0;i<n;i++) if(!inDegree[i]) {Q.push(i); minTime[i]=time[i];}
while (!Q.empty())
{
int u = Q.front();
Q.pop();
for (int v: G[u])
{
minTime[v] = max(minTime[v], minTime[u]+time[v]);
inDegree[v]--;
if (!inDegree[v]) Q.push(v);
}
}
return *max_element(minTime.begin(),minTime.end());
}
};