Problem Statement:

The n-queens puzzle is the problem of placing n queens on an n x n chessboard such that no two queens attack each other.

Given an integer n, return all distinct solutions to the n-queens puzzle. You may return the answer in any order.

Each solution contains a distinct board configuration of the n-queens' placement, where 'Q' and '.' both indicate a queen and an empty space, respectively.

Example 1:

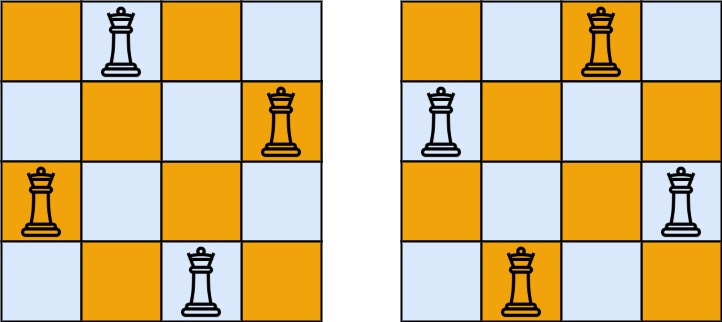
Input: n = 4
Output: [[".Q..","...Q","Q...","..Q."],["..Q.","Q...","...Q",".Q.."]]
Explanation: There exist two distinct solutions to the 4-queens puzzle as shown above

Example 2:

Input: n = 1
Output: [["Q"]]

Constraints:

1 <= n <= 9

Solution:

We will use some notations. We will denote a chess board configuration by an int array of size n such that value at each index in the array denotes the column number at which queen piece is present in the row number equal to index.

For example consider consider n=4. Then the array [0,2,1,3] denotes the following chessboard configuation:

 
Q...
..Q.
.Q..
...Q

Using this notation, suppose we have already placed the queen pieces for the first few rows. Now we have to check which column works for the next row. We just check each column one by one for validity. If a column number works, we assign it to that row and move on to the next row and if it does not work, we backtrack and mark that particular row as unassigned. Thus we are able to backtrack the entire path whenever we go wrong.

After we are done, we change output to the format required in the problem.

 
class Solution {
public:
    bool validate(vector<int>board, int row, int col, int sz)
    {
        for (int i=0; i<sz; i++)
        {
            if (i==row) continue;
            int j = board[i];
            if (j==-1) continue;
            if (j==col) return false;
            if ((j-col)==(row-i)) return false;
            if ((j-col)==(i-row)) return false;
        }
        return true;
    }
    void solve(int n, int row, vector<int>&board, vector<vector<int>>&boards)
    {
        if (row==n) boards.push_back(board);
        for (int col=0; col<n; col++)
        {
            if (validate(board,row,col,n))
            {
                board[row] = col;
                solve(n, row+1, board, boards);
                board[row] = -1;
            }
        }
        return;
    }
    vector<vector<string>> solveNQueens(int n) 
    {
        vector<int> board(n,-1);
        vector<vector<int>> boards;
        solve(n,0,board,boards);

        vector<vector<string>> res;
        for(auto config: boards)
        {
            vector<string> chessB(n, string(n,'.'));
            for(int i=0; i<n; i++) chessB[i][config[i]] = 'Q';
            res.push_back(chessB);
        }
        return res;
    }
};

Note: One crucial difference from the sudoku solver and this problem is that in sudoku solver only single solution was possible. Hence we could use bool as the return type in solve and return true whenever we found a valid sudoku whereas here, we need to keep going even if we have found a valid configuration and try more possibilities.