Problem Statement:

You are given an integer n. There is an undirected graph with n vertices, numbered from 0 to n - 1. You are given a 2D integer array edges where edges[i] = [a_i, b_i] denotes that there exists an undirected edge connecting vertices a_i and b_i.

Return the number of complete connected components of the graph.

A connected component is a subgraph of a graph in which there exists a path between any two vertices, and no vertex of the subgraph shares an edge with a vertex outside of the subgraph.

A connected component is said to be complete if there exists an edge between every pair of its vertices.

Example 1:

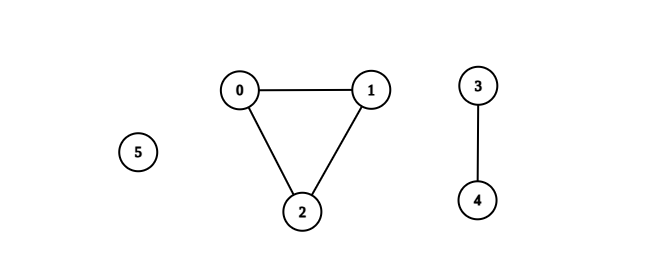
Input: n = 6, edges = [[0,1],[0,2],[1,2],[3,4]]
Output: 3
Explanation: From the picture above, one can see that all of the components of this graph are complete.

Example 2:

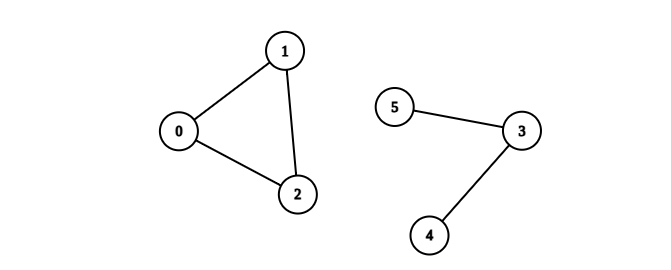
Input: n = 6, edges = [[0,1],[0,2],[1,2],[3,4],[3,5]]
Output: 1
Explanation: The component containing vertices 0, 1, and 2 is complete since there is an edge between every pair of two vertices. On the other hand, the component containing vertices 3, 4, and 5 is not complete since there is no edge between vertices 4 and 5. Thus, the number of complete components in this graph is 1.

Constraints:

1 <= n <= 50
0 <= edges.length <= n * (n - 1) / 2
edges[i].length == 2
0 <= a_i, b_i <= n - 1
a_i != b_i
There are no repeated edges.

Solution:

In any solution, all we need to do is count the number of nodes and edges in each connected component and increment answer every time $E = \frac12 * V * (V-1) $ where $E$ is the number of edges and $V$ is the nubmber of vertices in the connected component. Here I am providing DFS, BFS and DSU implmentations. In DSU implementation, I am using DSU with union by rank and path compression method which is the fastest in my experience. Read more about it here.

DSU solution:

 
class UnionFind
{
    vector<int> roots, ranks, edges;
public:
    UnionFind(int sz): roots(sz),ranks(sz),edges(sz)
    {
        for(int i=0; i<sz; i++)
        {
            roots[i]=i;
            ranks[i]=0;
            edges[i]=0;
        }
    }
    void unionSet(int x, int y)
    {
        int rootX=find(x);
        int rootY=find(y);
        edges[rootX]++;
        if (rootX==rootY) return;
        if (ranks[rootX]==ranks[rootY])ranks[rootX]++;
        if (ranks[rootX] <ranks[rootY]) swap(rootX,rootY);
        roots[rootY] = rootX;
        edges[rootX] += edges[rootY];
    }
    int find(int x)
    {
        if (x==roots[x]) return x;
        return roots[x] = find(roots[x]);
    }
    int getAnswer()
    {
        int res=0;
        unordered_map<int,int>H;
        for(int i=0; i<roots.size(); i++) H[find(i)]++;
        for (auto &[root, numNodes]: H)
        {
            int numEdges = edges[root];
            if (numEdges == numNodes*(numNodes-1)/2) res++;
        }
        return res;
    }
};
class Solution {
public:
    int countCompleteComponents(int n, vector<vector<int>>& edges) 
    {
        UnionFind uf = UnionFind(n);
        for(auto &edge: edges)
        {
            int u=edge[0], v=edge[1];
            uf.unionSet(u,v);
        }
        return uf.getAnswer();
    }
};

DFS solution:

 
class Solution {
public:
    void dfs(vector<vector<int>>&G, int u, unordered_set<int>&component, int &ctr)
    {
        component.insert(u);
        ctr += G[u].size();
        for (int v: G[u]) if (!component.count(v)) dfs(G, v, component, ctr);
    }
    int countCompleteComponents(int n, vector<vector<int>>& edges) {
        vector<vector<int>> G(n);
        for(auto &edge: edges)
        {
            int u=edge[0], v=edge[1];
            G[u].push_back(v);
            G[v].push_back(u);
        }
        unordered_set<int> visited, component;
        int ctr=0, res=0;
        for (int i=0; i<n; i++)
        {
            if (visited.count(i)) continue;
            dfs(G, i, component, ctr);
            ctr/=2; int nc=component.size();
            if (ctr==nc*(nc-1)/2) res++;
            visited.insert(component.begin(),component.end());
            component.clear(); ctr=0;
        }
        return res;
    }
};

BFS solution:

 
class Solution {
public:
    int countCompleteComponents(int n, vector<vector<int>>& edges) 
    {
        vector<vector<int>> G(n);
        for (auto &edge: edges)
        {
            int u=edge[0], v=edge[1];
            G[u].push_back(v);
            G[v].push_back(u);
        }
        queue<int> Q;
        vector<int> visited(n,false);
        int res = 0;
        for (int i=0; i<n; i++)
        {
            if (visited[i]) continue;
            int nodeCtr=0, edgeCtr=0;
            visited[i] = true;
            Q.push(i);
            nodeCtr++;
            while(!Q.empty())
            {
                for (int j=Q.size(); j>0; j--)
                {
                    int cur = Q.front();
                    Q.pop();
                    edgeCtr += G[cur].size();
                    for (int nbd: G[cur]) if (!visited[nbd])
                    {
                        visited[nbd] = true;
                        Q.push(nbd);
                        nodeCtr++;
                    }
                }
            }
            if (edgeCtr/2==(nodeCtr-1)*nodeCtr/2) res++;
        }
        return res;
    }
};

In DFS and BFS, we put (edgeCtr/2) because we are counting each edge twice.