Minimize the Total Price of the Trips - DFS + DP solution with explanation
Problem Statement:
There exists an undirected and unrooted tree with n nodes indexed from 0 to n - 1. You are given the integer n and a 2D integer array edges of length n - 1, where edges[i] = [ai, bi] indicates that there is an edge between nodes ai and bi in the tree.
Each node has an associated price. You are given an integer array price, where price[i] is the price of the ith node.
The price sum of a given path is the sum of the prices of all nodes lying on that path.
Additionally, you are given a 2D integer array trips, where trips[i] = [starti, endi] indicates that you start the ith trip from the node starti and travel to the node endi by any path you like.
Before performing your first trip, you can choose some non-adjacent nodes and halve the prices.
Return the minimum total price sum to perform all the given trips.
Example 1:
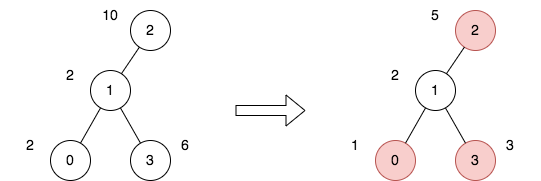
Input: n = 4, edges = [[0,1],[1,2],[1,3]], price = [2,2,10,6], trips = [[0,3],[2,1],[2,3]] Output: 23 Explanation: The diagram above denotes the tree after rooting it at node 2. The first part shows the initial tree and the second part shows the tree after choosing nodes 0, 2, and 3, and making their price half. For the 1st trip, we choose path [0,1,3]. The price sum of that path is 1 + 2 + 3 = 6. For the 2nd trip, we choose path [2,1]. The price sum of that path is 2 + 5 = 7. For the 3rd trip, we choose path [2,1,3]. The price sum of that path is 5 + 2 + 3 = 10. The total price sum of all trips is 6 + 7 + 10 = 23. It can be proven, that 23 is the minimum answer that we can achieve.
Example 2:
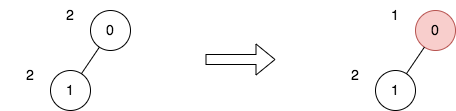
Input: n = 2, edges = [[0,1]], price = [2,2], trips = [[0,0]] Output: 1 Explanation: The diagram above denotes the tree after rooting it at node 0. The first part shows the initial tree and the second part shows the tree after choosing node 0, and making its price half. For the 1st trip, we choose path [0]. The price sum of that path is 1. The total price sum of all trips is 1. It can be proven, that 1 is the minimum answer that we can achieve.
Constraints:
1 <= n <= 50edges.length == n - 10 <= ai, bi <= n - 1edgesrepresents a valid tree.price.length == nprice[i]is an even integer.1 <= price[i] <= 10001 <= trips.length <= 1000 <= starti, endi <= n - 1
Solution:
There are 2 steps in the solution:
- Finding the route for each trip and after finishing all trips, we must have data of which node occurred how many times in all trips combined. Note that the graph has a tree structure, so we can be sure that there is a unique route for each trip. Let us call this data as
contribwhich is array of sizenand stores contributions of each node to the trips (combined). - Finding the minimum price for all these trips keeping the halving rule in mind.
Step 1 is pretty straightforward. For each trip, you just run DFS starting from source with appending current node in an array and if you meet the destination you have found the route.
In step 2, we run DFS again from node 0. Note that at any point during the DFS, if the parent node price was halved, then we have no choice but to return current node price without halving. But if the parent node price was not halved, we can either choose to halve or not halve the current node price and so we return the minimum of both choices. We maintain a 2-D array of size (n,2) to memoize results. Since, we are assuming node 0 has no parent and in the final answer price of node 0 may or may not be halved so we return dfs(cur=0, par=-1, parHalved=false).
void getContrib(vector<vector<int>>&G, vector<int>&contrib, vector<int>path, int cur, int dest, int par)
{
path.push_back(cur);
if (cur==dest)
{
for (int node: path) contrib[node]++;
return;
}
for (int nbd: G[cur])
{
if (nbd==par) continue;
getContrib(G, contrib, path, nbd, dest, cur);
}
path.pop_back();
}
int dfs(vector<vector<int>>&G, vector<vector<int>>&memo, vector<int>&contrib, vector<int>& prices, int cur, int par, bool parHalved)
{
if (memo[cur][parHalved]!=-1) return memo[cur][parHalved];
int resCurNotHalved = prices[cur]*contrib[cur];
for (int nbd: G[cur]) if(nbd!=par)
resCurNotHalved += dfs(G, memo, contrib, prices, nbd, cur, false);
if (parHalved) return memo[cur][true] = resCurNotHalved;
int resCurHalved = prices[cur]*contrib[cur]/2;
for (int nbd: G[cur]) if(nbd!=par)
resCurHalved += dfs(G, memo, contrib, prices, nbd, cur, true);
return memo[cur][false] = min(resCurNotHalved, resCurHalved);
}
int minimumTotalPrice(int n, vector<vector<int>>& edges, vector<int>& price, vector<vector<int>>& trips)
{
vector<vector<int>> G(n, vector<int>{});
for (auto &edge: edges)
{
int u=edge[0], v=edge[1];
G[u].push_back(v);
G[v].push_back(u);
}
vector<int> contrib(n, 0);
for (auto &trip: trips)
{
int src=trip[0], dest=trip[1];
vector<int> path;
getContrib(G, contrib, path, src, dest, -1);
}
vector<vector<int>> memo(n, vector<int>(2, -1));
return dfs(G, memo, contrib, price, 0, -1, false);
}