Array     C++     Dynamic Programming     Hard     Prefix Sum    

Problem Statement:

There are n piles of coins on a table. Each pile consists of a positive number of coins of assorted denominations.

In one move, you can choose any coin on top of any pile, remove it, and add it to your wallet.

Given a list piles, where piles[i] is a list of integers denoting the composition of the ith pile from top to bottom, and a positive integer k, return the maximum total value of coins you can have in your wallet if you choose exactly k coins optimally.

 

Example 1:

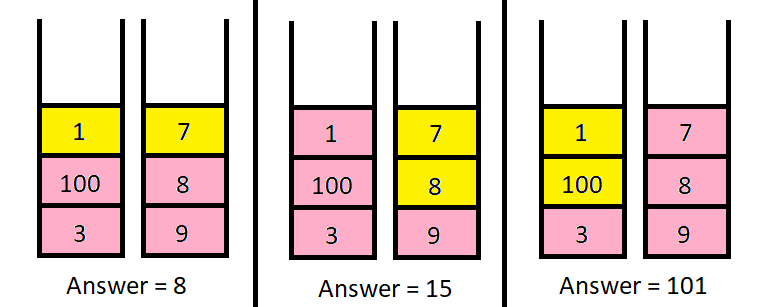
Input: piles = [[1,100,3],[7,8,9]], k = 2
Output: 101
Explanation:
The above diagram shows the different ways we can choose k coins.
The maximum total we can obtain is 101.

Example 2:

Input: piles = [[100],[100],[100],[100],[100],[100],[1,1,1,1,1,1,700]], k = 7
Output: 706
Explanation:
The maximum total can be obtained if we choose all coins from the last pile.

 

Constraints:

  • n == piles.length
  • 1 <= n <= 1000
  • 1 <= piles[i][j] <= 105
  • 1 <= k <= sum(piles[i].length) <= 2000

Solution:

We define dp[i][j] as the the answer considering 1st i piles for at most j coins. Hence final answer is dp[n][k]. In base case we consider i=0 ie considering zero piles. This row will be just zeroes. Similarly for j=0 column also, it will be all zeroes.

Consider any general dp[i][j].

We can take 0 coins from ith pile and all the j coins from the first i-1 piles. The value for this situation is dp[i-1][j] + 0.

We can also take 3 coins from ith pile (assume valid) and j-3 coins from the first i-1 piles. The value for this situation is dp[i-1][j-3] + piles[i-1][0]+piles[i-1][1]+piles[i-1][2].

Similarly we can have other possiblities as well. dp[i][j] is the maximum of all these possibilities.

We define cur as the number of coins we take from the current pile and curSum as the sum of values of these cur coins.

 
int maxValueOfCoins(vector<vector<int>>& piles, int k) 
{
    int n = piles.size();
    vector<vector<int>> dp(n+1, vector<int>(k+1, 0));
    for (int i=1; i<=n; i++)
    {
        for (int j=0; j<=k; j++)
        {
            dp[i][j] = dp[i-1][j]; // cur=0
            int curSum = 0;
            for (int cur=1; cur<=min((int)piles[i-1].size(),j); cur++)
            {
                curSum += piles[i-1][cur-1];
                dp[i][j] = max(dp[i][j], dp[i-1][j-cur]+curSum);
            }
        }
    }
    return dp[n][k];
}

\(TC= O(n\sum_{i=1}^n {P_i})\) where $P_i$ is the size of ith pile. \(SC: O(nk)\)