Problem Statement:

You are given a 0-indexed m x n integer matrix grid and an integer k. You are currently at position (0, 0) and you want to reach position (m - 1, n - 1) moving only down or right.

Return the number of paths where the sum of the elements on the path is divisible by k. Since the answer may be very large, return it modulo 10⁹ + 7.

Example 1:

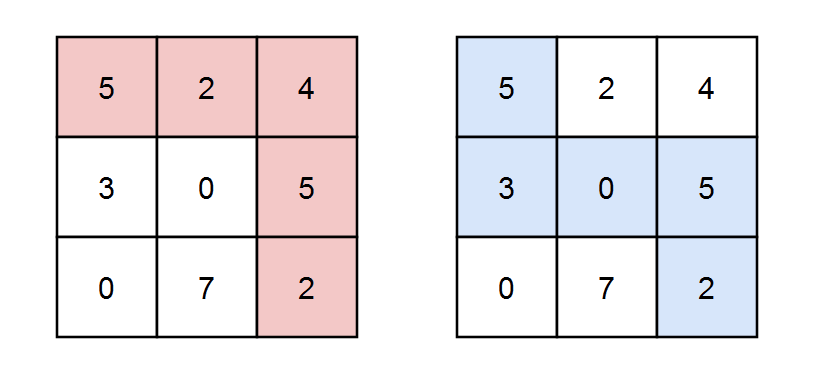
Input: grid = [[5,2,4],[3,0,5],[0,7,2]], k = 3
Output: 2
Explanation: There are two paths where the sum of the elements on the path is divisible by k.
The first path highlighted in red has a sum of 5 + 2 + 4 + 5 + 2 = 18 which is divisible by 3.
The second path highlighted in blue has a sum of 5 + 3 + 0 + 5 + 2 = 15 which is divisible by 3.

Example 2:

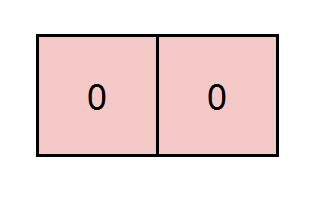
Input: grid = [[0,0]], k = 5
Output: 1
Explanation: The path highlighted in red has a sum of 0 + 0 = 0 which is divisible by 5.

Example 3:

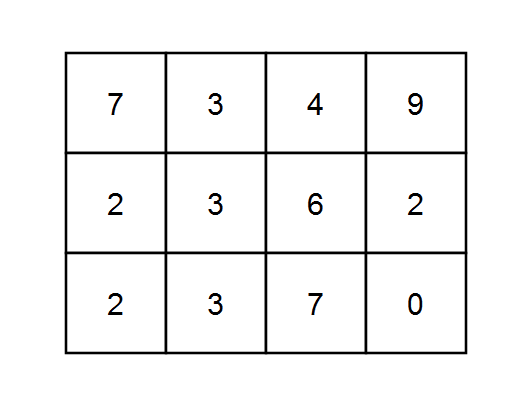
Input: grid = [[7,3,4,9],[2,3,6,2],[2,3,7,0]], k = 1
Output: 10
Explanation: Every integer is divisible by 1 so the sum of the elements on every possible path is divisible by k.

Constraints:

m == grid.length
n == grid[i].length
1 <= m, n <= 5 * 10⁴
1 <= m * n <= 5 * 10⁴
0 <= grid[i][j] <= 100
1 <= k <= 50

Solution:

Firstly a note regarding notation, I have replaced small k with capital K and I am using small k for indexing.

Algorithm:

We will create a DP table of shape (M,N,K) where dp[i][j][k] denotes number of ways to reach (i,j) coordinate with sum%K==k. At the end we will return dp[M-1][N-1][0].

Now for (0,0) there is one way to reach dp[0][0]%K but for other values of k, there is no way to achieve that sum.

Recurrence relation

 
dp[i][j][k] = A + B

where A is the number of ways to reach (i,j) via (i,j-1) and B is the number of ways to reach (i,j) via (i-1,j) Now we know that A = dp[i][j-1][idx]. We want to find this idx Suppose grid[i][j]%K==x. Then

 
idx = (K + k - x) % K

This idx value is same even for (i-1,j)

C++ code:

 
class Solution {
public:
    int numberOfPaths(vector<vector<int>>& grid, int K) 
    {
        int m=grid.size(), n=grid[0].size(), mod=1000000007;
        vector<vector<vector<int>>> dp(m, vector<vector<int>>(n,vector<int>(K,0)));
        dp[0][0][grid[0][0]%K]++;
        for (int i=0; i<m; i++)
            for (int j=0; j<n; j++)
                for (int k=0; k<K; k++)
                {
                    if (i==0 && j==0) continue;
                    int a = ((j==0) ? 0 : dp[i][j-1][(K+k-grid[i][j]%K)%K] % mod);
                    int b = ((i==0) ? 0 : dp[i-1][j][(K+k-grid[i][j]%K)%K] % mod);
                    dp[i][j][k] = (a+b)%mod;
                }
        return dp[m-1][n-1][0];
    }
};