Array     Binary Search     C++     Dynamic Programming     Hard     Sorting    

Problem Statement:

We have n jobs, where every job is scheduled to be done from startTime[i] to endTime[i], obtaining a profit of profit[i].

You're given the startTime, endTime and profit arrays, return the maximum profit you can take such that there are no two jobs in the subset with overlapping time range.

If you choose a job that ends at time X you will be able to start another job that starts at time X.

 

Example 1:

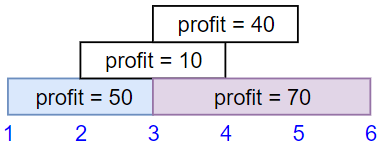
Input: startTime = [1,2,3,3], endTime = [3,4,5,6], profit = [50,10,40,70]
Output: 120
Explanation: The subset chosen is the first and fourth job. 
Time range [1-3]+[3-6] , we get profit of 120 = 50 + 70.

Example 2:

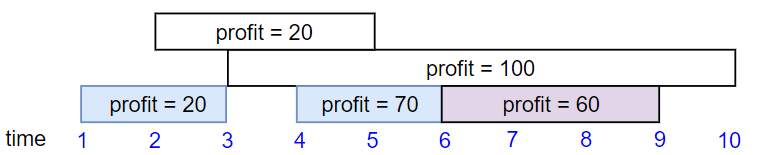
Input: startTime = [1,2,3,4,6], endTime = [3,5,10,6,9], profit = [20,20,100,70,60]
Output: 150
Explanation: The subset chosen is the first, fourth and fifth job. 
Profit obtained 150 = 20 + 70 + 60.

Example 3:

Input: startTime = [1,1,1], endTime = [2,3,4], profit = [5,6,4]
Output: 6

 

Constraints:

  • 1 <= startTime.length == endTime.length == profit.length <= 5 * 104
  • 1 <= startTime[i] < endTime[i] <= 109
  • 1 <= profit[i] <= 104

Solution:

Explanation

We sort the jobs by their ending times. Now as we traverse through the jobs array, we are going to apply a logic similar to Knapsack:

  • We maintain a dp array of (endTime,maxProfitTillHere) entities. We initialize it to [(0,0)].
  • For each job, we have two options: (i) To do this job: in this case we need to find the maxProfit till the time before the startTime of current job. (ii) Not do this job: in the case we will have the same maxProfittill the previous dp member.
  • This is equivalent to the two options we have in a knapsack problem.

Example

 
Input: startTime = [1,2,3,3], endTime = [3,4,5,6], profit = [50,10,40,70]

Then sorted by endTime, we will have

 
jobs = [(1,3,50),(2,4,10),(3,5,40),(3,6,70)]

Initialize dp:

 
dp = [(0,0)]`

At i=0,

 
option_A = 0+50
option_B = 0

dp gets appended.

 
dp = [(0,0),(3,50)]

At i=1, Job = (2,4,10):

 
option_A = 0+10
option_B = 50

dp remains same.

 
dp = [(0,0),(3,50)]

At i=2, Job = (3,5,40):

 
option_A = 50+40
option_B = 50

dp gets appended

 
dp = [(0,0),(3,50),(5,90)]

At i=3, Job = (3,6,70):

 
option_A = 50+70
option_B = 90

dp gets appended

 
dp = [(0,0),(3,50),(5,90),(6,120)]

Finally answer is 120.

For implementation we create a custom class Job. For the DP part, we just use startTime=-1 for all timestamps as it does not matter.

C++ code:

 
class Job
{
    public:
    int startTime, endTime, profit;
    Job(int s, int e, int p): startTime(s), endTime(e), profit(p) {}
    bool operator <  (const Job &other_job)const{return endTime  < other_job.endTime;}
    bool operator == (const Job &other_job)const{return endTime == other_job.endTime;}
};

class Solution {
public:
    int jobScheduling(vector<int>& startTime, vector<int>& endTime, vector<int>& profit) 
    {
        int n = startTime.size();
        vector<Job> jobs;
        for (int i=0; i<n; i++)
            jobs.push_back(Job(startTime[i],endTime[i],profit[i]));
        sort(jobs.begin(),jobs.end());
        
        vector<Job> dp = vector<Job>{Job(-1,0,0)};
        for (const Job &job: jobs)
        {
            auto itr = upper_bound(dp.begin(),dp.end(),Job(-1,job.startTime,-1));
            int idx = itr-dp.begin()-1;
            int opt_A = dp[idx].profit + job.profit;
            int opt_B = dp.rbegin()->profit;
            if (opt_A > opt_B)
                dp.push_back(Job(-1,job.endTime, opt_A));
        }
        return dp.rbegin()->profit;
    }
};