Problem Statement:

Given an m x n board of characters and a list of strings words, return all words on the board.

Each word must be constructed from letters of sequentially adjacent cells, where adjacent cells are horizontally or vertically neighboring. The same letter cell may not be used more than once in a word.

Example 1:

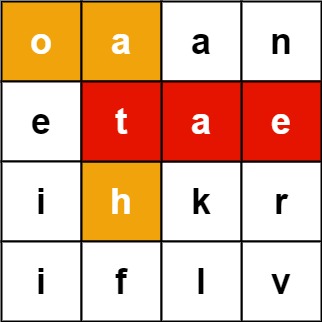
Input: board = [["o","a","a","n"],["e","t","a","e"],["i","h","k","r"],["i","f","l","v"]], words = ["oath","pea","eat","rain"]
Output: ["eat","oath"]

Example 2:

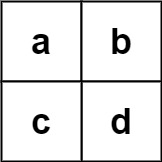
Input: board = [["a","b"],["c","d"]], words = ["abcb"]
Output: []

Constraints:

m == board.length
n == board[i].length
1 <= m, n <= 12
board[i][j] is a lowercase English letter.
1 <= words.length <= 3 * 10⁴
1 <= words[i].length <= 10
words[i] consists of lowercase English letters.
All the strings of words are unique.

Solution:

Step 1 is to build Trie. This should be simple enough if you have done this.

Step 2 is to do DFS and pass this Trie as an argument of DFS. In a simpler implemtation, you can pass the same trie that we constructed again and again and search from root using hasPrefix and hasWord to look for candidates but this will give you a TLE because it is traversing from the root node again and again. The more efficient way is to pass child trie in the recursive call, so we dont actually need hasPrefix or hasWord. Nevertheless I have left it as it helps us to understand Trie concept.

You might still get a TLE. Now, change the arguments board to pass only reference to avoid time of copying in memory for each recursive call.

This gives us an AC.

 

class Trie
{
    public:
    vector<Trie *> children = vector<Trie *>(26, NULL);
    bool isEnd = false;
    void insert(string word, int pos=0)
    {
        if (pos==word.length())
        {
            isEnd = true;
            return;
        }
        int idx = word[pos]-'a';
        if (children[idx]==NULL)
            children[idx] = new Trie;
        children[idx]->insert(word, pos+1);
    }
    bool hasPrefix(string prefix, int pos=0)
    {
        if (pos==prefix.length()) return true;
        int idx = prefix[pos]-'a';
        if (children[idx]==NULL) return false;
        return children[idx]->hasPrefix(prefix, pos+1);
    }
    bool hasWord(string word, int pos=0)
    {
        if (pos==word.length()) return isEnd;
        int idx = word[pos]-'a';
        if (children[idx]==NULL) return false;
        return children[idx]->hasWord(word, pos+1);
    }
};

class Solution {
public:
    void dfs(vector<vector<char>> &board, int i, int j, int m, int n, Trie *trie, unordered_set<string>&res,string &curr)
    {
        if (board[i][j]=='*') return;
        int idx = board[i][j]-'a';
        Trie *child_trie = trie->children[idx];
        if (child_trie==NULL) return;
        curr.push_back(board[i][j]);
        if (child_trie->isEnd) res.insert(curr);
        board[i][j] = '*';
        if (i-1>=0) dfs(board,i-1,j,m,n,child_trie,res,curr);
        if (i+1<m)  dfs(board,i+1,j,m,n,child_trie,res,curr);
        if (j-1>=0) dfs(board,i,j-1,m,n,child_trie,res,curr);
        if (j+1<n)  dfs(board,i,j+1,m,n,child_trie,res,curr);
        board[i][j] = 'a'+idx;
        curr.pop_back();
    }
    vector<string> findWords(vector<vector<char>>& board, vector<string>& words) 
    {
        Trie *trie = new Trie;
        for (string word: words)
            trie->insert(word);

        // Code for testing Trie
        // for (string w: vector<string>{"oat","oath","oaths","oas","aoth","eat"})
        //     cout << w << " hasPrefix: " << trie.hasPrefix(w) << " hasWord: " << trie.hasWord(w) << endl;

        int m=board.size(), n=board[0].size();
        unordered_set<string> res;
        for (int i=0; i<m; i++)
            for (int j=0; j<n; j++)
            {
                string cur="";
                dfs(board, i, j, m, n, trie, res, cur);
            }
        vector<string>resv;
        for(string s: res) resv.push_back(s);
        return resv;
    }
};

Note: My old code which gave TLE for large input can be found here. It is simpler in implementation but calls hasPrefix again and again which traverses from root everytime.