Linked List Cycle II - Floyd's Tortoise and Hare Algorithm
Problem Statement:
Given the head of a linked list, return the node where the cycle begins. If there is no cycle, return null.
There is a cycle in a linked list if there is some node in the list that can be reached again by continuously following the next pointer. Internally, pos is used to denote the index of the node that tail's next pointer is connected to (0-indexed). It is -1 if there is no cycle. Note that pos is not passed as a parameter.
Do not modify the linked list.
Example 1:
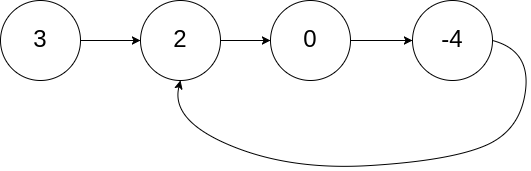
Input: head = [3,2,0,-4], pos = 1 Output: tail connects to node index 1 Explanation: There is a cycle in the linked list, where tail connects to the second node.
Example 2:
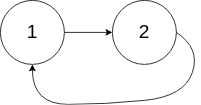
Input: head = [1,2], pos = 0 Output: tail connects to node index 0 Explanation: There is a cycle in the linked list, where tail connects to the first node.
Example 3:

Input: head = [1], pos = -1 Output: no cycle Explanation: There is no cycle in the linked list.
Constraints:
- The number of the nodes in the list is in the range
[0, 104]. -105 <= Node.val <= 105posis-1or a valid index in the linked-list.
Follow up: Can you solve it using O(1) (i.e. constant) memory?
Solution:
Consider a situation like this.

Consider two pointers tortoise and hare which move at 1x and 2x respectively.
We know that d(hare)=2d(tortoise). So, when they meet we have:
F+nC+a = 2(F+a)
LHS is for hare and RHS is for tortoise.
Then we make the tortoise start again from the beginning and hare from the meeting position itself but both at 1x. Then they meet exactly at the cycle start point because after F steps, tortoise is at F and hare is at F+a+F. But we know that F+a=nC from earlier equation. Hence hare is also at F and this node is the answer.
class Solution {
public:
ListNode *detectCycle(ListNode *head) {
ListNode *tortoise=head, *hare=head;
while(1)
{
if (!hare||!hare->next) return NULL;
tortoise = tortoise->next;
hare = hare->next->next;
if (tortoise==hare) break;
}
tortoise = head;
while (tortoise!=hare)
{
tortoise = tortoise->next;
hare = hare->next;
}
return hare;
}
};
There is obviously also an easier O(N) space HashSet solution that gives you an AC but I think the Floyd’s algo solution is more useful in real life interview. For the sake of completion here is the HashSet solution:
class Solution {
public:
ListNode *detectCycle(ListNode *head) {
unordered_set<ListNode *> S;
while (head)
{
if (S.count(head)) return head;
S.insert(head);
head = head->next;
}
return NULL;
}
};