Array     C++     Greedy     Matrix     Medium     Sorting    

Problem Statement:

You are given a binary matrix matrix of size m x n, and you are allowed to rearrange the columns of the matrix in any order.

Return the area of the largest submatrix within matrix where every element of the submatrix is 1 after reordering the columns optimally.

 

Example 1:

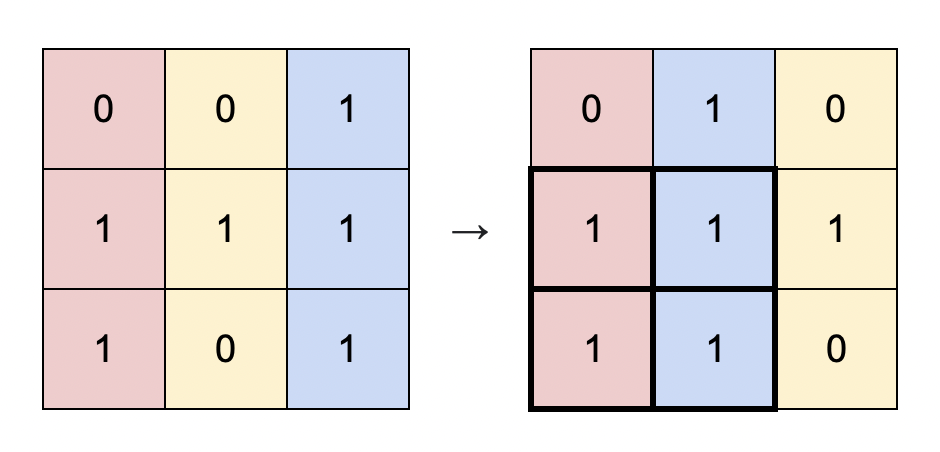
Input: matrix = [[0,0,1],[1,1,1],[1,0,1]]
Output: 4
Explanation: You can rearrange the columns as shown above.
The largest submatrix of 1s, in bold, has an area of 4.

Example 2:

Input: matrix = [[1,0,1,0,1]]
Output: 3
Explanation: You can rearrange the columns as shown above.
The largest submatrix of 1s, in bold, has an area of 3.

Example 3:

Input: matrix = [[1,1,0],[1,0,1]]
Output: 2
Explanation: Notice that you must rearrange entire columns, and there is no way to make a submatrix of 1s larger than an area of 2.

 

Constraints:

  • m == matrix.length
  • n == matrix[i].length
  • 1 <= m * n <= 105
  • matrix[i][j] is either 0 or 1.

Solution:

Suppose you have a histogram represented by array histogram where histogram[i] denotes height of bar at ith position. We can permute the histogram in any order we want and we would like to know what is the largest area possible. How do we solve this?

Well, we can just sort the array histogram in reverse and check for histogram[i]*(i+1) since all i+1 bars from 0 to i, both included, have heights equal to more than histogram[i].

 
int findMaxArea(vector<int> histogram)
{
    sort(histogram.rbegin(),histogram.rend()); // sort in reverse
    int maxArea = 0;
    for (int i=0; i<histogram.size(); i++)
        maxArea = max(maxArea, histogram[i]*(i+1));
    return maxArea;
}

Now we use this logic in our situation. We can treat each row as the base of histogram going upto the top or till we see a zero. Consider the following input matrix:

 
0 0 1
1 1 1
1 0 1

From here, we can get the following matrix as heights:

 
0 0 1
1 1 2
2 0 3

Each row can be treated as a histogram and from here we apply the logic discussed earlier to find the answer.

 
class Solution {
public:
    int largestSubmatrix(vector<vector<int>>& matrix) 
    {
        int n = matrix.size(), m = matrix[0].size();
        vector<vector<int>> heights(n, vector<int>(m,0));
        for(int i=0; i<n; i++) for(int j=0; j<m; j++) 
          if(matrix[i][j]) heights[i][j] = (i==0) ? 1 : 1 + heights[i-1][j];
        int res = 0;
        for(int i=0; i<n; i++)
        {
            vector<int> histogram = heights[i];
            sort(histogram.rbegin(),histogram.rend());
            for(int j=0; j<m && histogram[j]; j++) res = max(res, histogram[j]*(j+1));
        }
        return res;
    }
};

$TC: O(n m\log(m))$, $SC: O(nm)$