Array     C++     Heap (Priority Queue)     Medium     Ordered Map     Sorting    

Problem Statement:

Given a 2D integer array nums, return all elements of nums in diagonal order as shown in the below images.

 

Example 1:

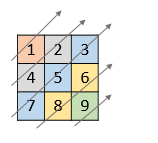
Input: nums = [[1,2,3],[4,5,6],[7,8,9]]
Output: [1,4,2,7,5,3,8,6,9]

Example 2:

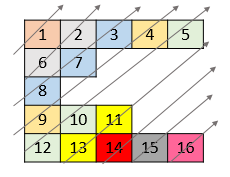
Input: nums = [[1,2,3,4,5],[6,7],[8],[9,10,11],[12,13,14,15,16]]
Output: [1,6,2,8,7,3,9,4,12,10,5,13,11,14,15,16]

 

Constraints:

  • 1 <= nums.length <= 105
  • 1 <= nums[i].length <= 105
  • 1 <= sum(nums[i].length) <= 105
  • 1 <= nums[i][j] <= 105

Solution:

Any solution for this question has to be based on a simple observation that each diagnoal contains sum of indices as same. For example in the first example of 3 by 3 grid we have the following diagonals in order:

 
(0,0) -> sum is 0
(1,0),(0,1) -> sum is 1
(2,0),(1,1),(0,2) -> sum is 2
(2,1),(1,2) -> sum is 3
(2,2) -> sum is 4

Now, We create an ordered map or a TreeMap to store numbers. We store nums[i][j] at the key (i+j). Now we can use this to construct res.

This gives us the following solution which is just 5 lines of code.

 
vector<int> findDiagonalOrder(vector<vector<int>>& nums) 
{
    map<int,vector<int>>H; 
    vector<int>res;
    for(int i=0; i<nums.size(); i++) for(int j=0; j<nums[i].size(); j++) H[i+j].push_back(nums[i][j]);        
    for (auto &[k,v]:H) for(int i=v.size()-1; i>=0; i--) res.push_back(v[i]);
    return res;
}

$TC: O(N+M)$ where $N$ is the size of nums and M is the maximum length of nums[i] for $0<=i<N$

EDIT: I wrote another solution which is even more efficient and does not require TreeMap and works using just a 2-D intermediate array. The idea is similar. We take advantage of the fact that when we encounter a sum of indices s for the first time say at (i,j), we have already seen at least one number with sum of indices s-1 at (i,j-1) , and no number with the sum of indices s+1, so we can just insert single member 1-D array {nums[i][j]} at the end because this will the index i+j of H. In other cases we add nums[i][j] to H[i+j].

 
vector<int> findDiagonalOrder(vector<vector<int>>& nums) 
{
    vector<vector<int>>H;
    for(int i=0; i<nums.size(); i++) for(int j=0; j<nums[i].size(); j++)
        if (H.size()==i+j)H.push_back({nums[i][j]});
        else H[i+j].push_back(nums[i][j]);
    vector<int> res;
    for (auto &v:H) for(int i=v.size()-1; i>=0; i--) res.push_back(v[i]);
    return res;
}