Bulb Switcher - Easy explanation
Problem Statement:
There are n bulbs that are initially off. You first turn on all the bulbs, then you turn off every second bulb.
On the third round, you toggle every third bulb (turning on if it's off or turning off if it's on). For the ith round, you toggle every i bulb. For the nth round, you only toggle the last bulb.
Return the number of bulbs that are on after n rounds.
Example 1:
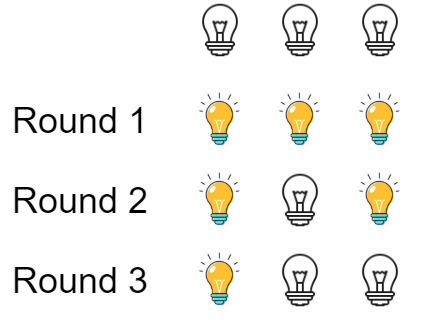
Input: n = 3 Output: 1 Explanation: At first, the three bulbs are [off, off, off]. After the first round, the three bulbs are [on, on, on]. After the second round, the three bulbs are [on, off, on]. After the third round, the three bulbs are [on, off, off]. So you should return 1 because there is only one bulb is on.
Example 2:
Input: n = 0 Output: 0
Example 3:
Input: n = 1 Output: 1
Constraints:
0 <= n <= 109
Solution:
Consider ith bulb (1-indexed) and consider how many times it will be flipped. The answer is it will be flipped at step number of all of its factors.
For example:
1->1
2->1,2
3->1,3
4->1,2,4
5->1,5
6->1,2,3,6
7->1,7
8->1,2,4,8
9->1,3,9
10->1,2,5,10
Hence, if i has even number of factors, it will eventually return to its initial state however if i has odd number of factors, it will be eventually be in flipped states. This odd number of factors also correspnds to perfect squares.
Hence, essentially the problem translates to “How many perfect squares in the [1,n] range?”.
Here is a straightforward solution using sqrt from cmath.
int bulbSwitch(int n)
{
return (int)sqrt((double)n);
}
Now complexity of sqrt is $O(1)$ because it uses FISR method. Read my gist for more details on FISR method.
Following solution is $O(\log(n))$ method for finding integer square root.
int bulbSwitch(int n)
{
if (n==0) return n;
if (n<4) return 1;
int lo=0, hi=n/2, mid;
while (lo<=hi)
{
mid = lo + (hi-lo)/2;
if (n/mid==mid) return mid;
else if (n/mid > mid) lo = mid+1;
else if (n/mid < mid) hi = mid-1;
}
return lo-1;
}