Problem Statement:

Given the root of a binary tree, replace the value of each node in the tree with the sum of all its cousins' values.

Two nodes of a binary tree are cousins if they have the same depth with different parents.

Return the root of the modified tree.

Note that the depth of a node is the number of edges in the path from the root node to it.

Example 1:

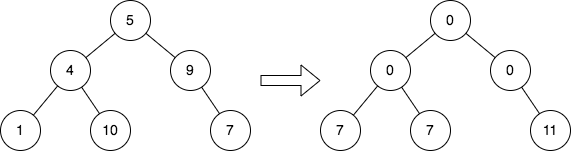
Input: root = [5,4,9,1,10,null,7]
Output: [0,0,0,7,7,null,11]
Explanation: The diagram above shows the initial binary tree and the binary tree after changing the value of each node.
- Node with value 5 does not have any cousins so its sum is 0.
- Node with value 4 does not have any cousins so its sum is 0.
- Node with value 9 does not have any cousins so its sum is 0.
- Node with value 1 has a cousin with value 7 so its sum is 7.
- Node with value 10 has a cousin with value 7 so its sum is 7.
- Node with value 7 has cousins with values 1 and 10 so its sum is 11.

Example 2:

Input: root = [3,1,2]
Output: [0,0,0]
Explanation: The diagram above shows the initial binary tree and the binary tree after changing the value of each node.
- Node with value 3 does not have any cousins so its sum is 0.
- Node with value 1 does not have any cousins so its sum is 0.
- Node with value 2 does not have any cousins so its sum is 0.

Constraints:

The number of nodes in the tree is in the range [1, 10⁵].
1 <= Node.val <= 10⁴

Solution:

DFS solution: We use DFS twice. First time, to recursively compute level sums. During second time, for any node at level value level we modify values of level level+1 as follows:

 
int cousinSum = levels[level+1] - node->left - node->right;
node->left->val = node->right-val = cousinSum;

Complete DFS solution:

 
void dfsA(TreeNode *root, vector<int>&levels, int level)
{
    if (!root) return;
    if (levels.size()==level) levels.push_back(0);
    levels[level] += root->val;
    dfsA(root->left, levels, level+1);
    dfsA(root->right, levels, level+1);
}
void dfsB(TreeNode *root, vector<int> &levels, int level)
{
    if (!root) return;
    int cur = 0;
    if (root->left) cur += root->left->val;
    if (root->right) cur += root->right->val;
    if(root->left) root->left->val = levels[level+1]-cur;
    if (root->right) root->right->val = levels[level+1]-cur;
    dfsB(root->left, levels, level+1);
    dfsB(root->right, levels, level+1);
}
TreeNode* replaceValueInTree(TreeNode* root) 
{
    vector<int> levels;
    dfsA(root, levels, 0);
    dfsB(root, levels, 0);
    root->val = 0;
    return root;
}

BFS solution: We can also modify BFS to do the same thing. During the traversal, instead of adding node values at current level, we add node values at next level. Then, we can use the equation described earlier to compute the same thing.

Complete BFS solution:

 
TreeNode* replaceValueInTree(TreeNode* root) 
{
    queue<TreeNode*> Q;
    Q.push(root);
    while(!Q.empty())
    {
        int curSum = 0;
        vector<TreeNode*> levelNodes;
        for (int i=Q.size(); i>0; i--)
        {
            TreeNode* cur = Q.front();
            Q.pop();
            levelNodes.push_back(cur);
            if (cur->left)
            {
                curSum += cur->left->val;
                Q.push(cur->left);
            }
            if (cur->right)
            {
                curSum += cur->right->val;
                Q.push(cur->right);
            }
        }
        for (TreeNode* node: levelNodes)
        {
            int cousinSum = curSum;
            if (node->left) cousinSum -= node->left->val;
            if (node->right) cousinSum -= node->right->val;
            if (node->left) node->left->val = cousinSum;
            if (node->right) node->right->val = cousinSum;
        }
    }
    root->val = 0;
    return root;
}