Problem Statement:

You are given a positive integer n, indicating that we initially have an n x n 0-indexed integer matrix mat filled with zeroes.

You are also given a 2D integer array query. For each query[i] = [row1_i, col1_i, row2_i, col2_i], you should do the following operation:

Add 1 to every element in the submatrix with the top left corner (row1_i, col1_i) and the bottom right corner (row2_i, col2_i). That is, add 1 to mat[x][y] for all row1_i <= x <= row2_i and col1_i <= y <= col2_i.

Return the matrix mat after performing every query.

Example 1:

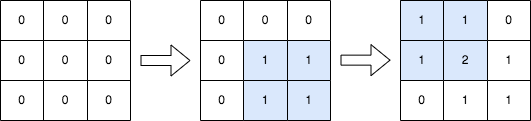
Input: n = 3, queries = [[1,1,2,2],[0,0,1,1]]
Output: [[1,1,0],[1,2,1],[0,1,1]]
Explanation: The diagram above shows the initial matrix, the matrix after the first query, and the matrix after the second query.
- In the first query, we add 1 to every element in the submatrix with the top left corner (1, 1) and bottom right corner (2, 2).
- In the second query, we add 1 to every element in the submatrix with the top left corner (0, 0) and bottom right corner (1, 1).

Example 2:

Input: n = 2, queries = [[0,0,1,1]]
Output: [[1,1],[1,1]]
Explanation: The diagram above shows the initial matrix and the matrix after the first query.
- In the first query we add 1 to every element in the matrix.

Constraints:

1 <= n <= 500
1 <= queries.length <= 10⁴
0 <= row1_i <= row2_i < n
0 <= col1_i <= col2_i < n

Solution:

Intuition

We will maintain a matrix where each update is O(1) in time. At the end, we will use cumulative sum method to get final output.

Approach

Let us first solve the 1-D version of the problem. Also availabe here. I will give a brief overview. Problem is given length of array N starting with all zeros and some update queries of format (left,right,increment), return the final array.

 
Input: length = 5, updates = [[1,3,2],[2,4,3],[0,2,-2]]

A naive way would be to update from left to right for each query:

 
vector<int> solve(int n, vector<vector<int>> updates)
{
    vector<int> A(n,0);
    for (auto &query: updates)
    {
        int left = query[0], right = query[1], increment = query[2];
        for (int i=left; i<=right; i++) A[i]+=increment;
    }
    return A;
}

Here is a smarter way to do this: we just do +increment at left and -increment at right+1 and finally return the cumulative sum array. We will need array of length N+1 this time.

 
vector<int> solve(int n, vector<vector<int>> updates)
{
    vector<int> A(n+1,0);
    for (auto &query: updates)
    {
        int left = query[0], right = query[1], increment = query[2];
        A[left]+=increment;
        A[right+1]-=increment
    }
    for (int i=1; i<=n; i++) A[i]+=A[i-1];
    A.pop_back(); // we want only first n items. A[n] is always zero
    return A;
}

You can see that the first method is $O(Q*N)$ and second method is $O(Q+N)$ where N is size of array and Q is number of update queries.

Let us extend this logic to our problem. Here we will do the following updates for each update query.

 
M[r1][c1]++;
M[r2+1][c1]--;
M[r1][c2+1]--;
M[r2+1][c2+1]++;

The reason we need to do like this is because here we will be taking a 2-D cumulative sum by which we mean $res[i][j] = \sum_{ii,jj} M[ii][jj]$ where $0<=ii<=i$ and $0<=jj<=j$

Complexity

Time complexity: $O(Q + N^2)$
Space complexity: $O(N^2)$

Code

 
class Solution {
public:
    vector<vector<int>> rangeAddQueries(int n, vector<vector<int>>& queries) 
    {
        vector<vector<int>> M = vector<vector<int>>(n+1, vector<int>(n+1,0));
        for (auto &q: queries)
        {
            int r1=q[0], c1=q[1], r2=q[2], c2=q[3];
            M[r1][c1]++;
            M[r2+1][c1]--;
            M[r1][c2+1]--;
            M[r2+1][c2+1]++;
        }
        // Use this to print update matrix. You can check manually that the 2-D cumulative sum of this gives the answer
        // for (auto &v: M){for(int k: v)cout<<k<<',';cout<<endl;} 
        vector<vector<int>> res = vector<vector<int>>(n, vector<int>(n,0));
        res[0][0] = M[0][0];
        for (int i=1; i<n; i++) res[i][0]=res[i-1][0]+M[i][0];
        for (int j=1; j<n; j++) res[0][j]=res[0][j-1]+M[0][j];
        for (int i=1; i<n; i++) for (int j=1; j<n; j++)
            res[i][j] = -res[i-1][j-1]+res[i][j-1]+res[i-1][j]+M[i][j];
        return res;
    }
};