Problem Statement:

You are given an m x n grid where each cell can have one of three values:

0 representing an empty cell,
1 representing a fresh orange, or
2 representing a rotten orange.

Every minute, any fresh orange that is 4-directionally adjacent to a rotten orange becomes rotten.

Return the minimum number of minutes that must elapse until no cell has a fresh orange. If this is impossible, return -1.

Example 1:

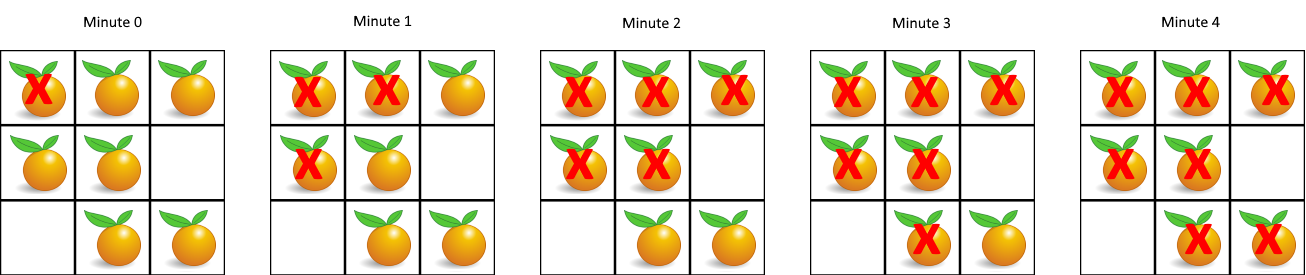
Input: grid = [[2,1,1],[1,1,0],[0,1,1]]
Output: 4

Example 2:

Input: grid = [[2,1,1],[0,1,1],[1,0,1]]
Output: -1
Explanation: The orange in the bottom left corner (row 2, column 0) is never rotten, because rotting only happens 4-directionally.

Example 3:

Input: grid = [[0,2]]
Output: 0
Explanation: Since there are already no fresh oranges at minute 0, the answer is just 0.

Constraints:

m == grid.length
n == grid[i].length
1 <= m, n <= 10
grid[i][j] is 0, 1, or 2.

Solution:

BFS is very appropriate here. We just need to check how many times we need to traverse to finish the queue. In one traversal, all adjacent members of the current queue get covered. At the end we also check thre is a fresh orange, if yes we return -1 and if not we return the answer.

Add all cells with rotten oranges in Queue.
Run BFS in the queue.
Count the number of times we need to traverse.
After we are done, check for any fresh remaining orange.

C++ Code:

 
class Solution {
public:
    bool notdone(vector<vector<int>> &grid)
    {
        for (auto row: grid)
            for (int cell: row)
                if (cell==1)
                    return true;
        return false;
    }

    int orangesRotting(vector<vector<int>>& grid) 
    {
        if (!notdone(grid)) return 0;
        int m=grid.size(), n=grid[0].size(), ctr=0;
        vector<pair<int,int>> dirs { {-1,0},{1,0},{0,-1},{0,1} };
        queue<pair<int,int>> Q;
        for (int i=0; i<m; i++)
            for (int j=0; j<n; j++)
                if (grid[i][j]==2)
                    Q.push({i,j});
        while (!Q.empty())
        {
            int qsize = Q.size();
            for (int i=0; i<qsize; i++)
            {
                auto point = Q.front();
                Q.pop();
                for (auto dir: dirs)
                {
                    int x = point.first + dir.first;
                    int y = point.second + dir.second;
                    if (x<0 || x>=m || y<0 || y>=n || grid[x][y]!=1)
                        continue;
                    grid[x][y] = 2;
                    Q.push({x,y});
                }
            }
            ctr++;
        }
        if (notdone(grid)) return -1;
        return ctr-1;
    }
};