Binary Tree     Depth-First Search     Medium     Tree    

Problem Statement:

Given the root of a binary tree and an integer targetSum, return the number of paths where the sum of the values along the path equals targetSum.

The path does not need to start or end at the root or a leaf, but it must go downwards (i.e., traveling only from parent nodes to child nodes).

 

Example 1:

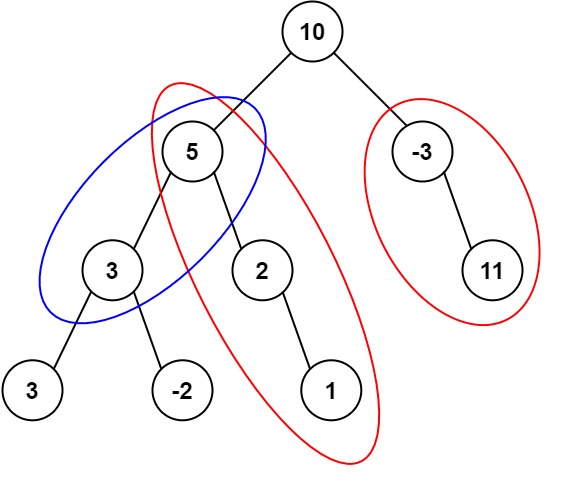
Input: root = [10,5,-3,3,2,null,11,3,-2,null,1], targetSum = 8
Output: 3
Explanation: The paths that sum to 8 are shown.

Example 2:

Input: root = [5,4,8,11,null,13,4,7,2,null,null,5,1], targetSum = 22
Output: 3

 

Constraints:

  • The number of nodes in the tree is in the range [0, 1000].
  • -109 <= Node.val <= 109
  • -1000 <= targetSum <= 1000

Solution:

The idea is that any valid path will have a starting node and go down thereafter. So, we start from root and go down while checking if there is valid path starting from that node. So, for the tree in the question example 1:

root = [10,5,-3,3,2,null,11,3,-2,null,1], targetSum = 8

We will check paths

[10],[10,5],[10,5,3],[10,5,3,3],[10,5,3,-2],[10,5,2],[10,5,2,1],[10,-3],[10,-3,11]

Then we will check paths

[5],[5,3],[5,3,3],[5,3,-2],[5,2],[5,2,1]

and so on.

C++ code:

class Solution {
public:
    int pathSum(TreeNode* root, int targetSum) 
    {
        if (!root) return 0;
        return sumUp(root, 0, targetSum) + pathSum(root->left, targetSum) + pathSum(root->right, targetSum);
    }
    int sumUp(TreeNode *root, long long curr, int target)
    {
        if (!root) return 0;
        curr += root->val;
        return (curr==target) + sumUp(root->left, curr, target) + sumUp(root->right,curr,target);
    }
};