Problem Statement:

Given an m x n grid of characters board and a string word, return true if word exists in the grid.

The word can be constructed from letters of sequentially adjacent cells, where adjacent cells are horizontally or vertically neighboring. The same letter cell may not be used more than once.

Example 1:

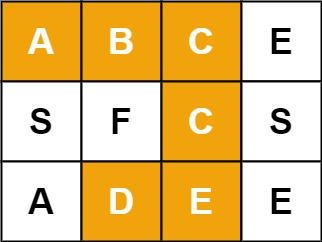
Input: board = [["A","B","C","E"],["S","F","C","S"],["A","D","E","E"]], word = "ABCCED"
Output: true

Example 2:

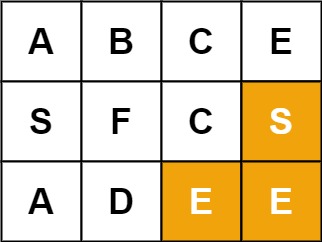
Input: board = [["A","B","C","E"],["S","F","C","S"],["A","D","E","E"]], word = "SEE"
Output: true

Example 3:

Input: board = [["A","B","C","E"],["S","F","C","S"],["A","D","E","E"]], word = "ABCB"
Output: false

Constraints:

m == board.length
n = board[i].length
1 <= m, n <= 6
1 <= word.length <= 15
board and word consists of only lowercase and uppercase English letters.

Follow up: Could you use search pruning to make your solution faster with a larger board?

Solution:

Like others my solution also uses DFS but I am getting TLE. It uses more memory than other approaches (to store copies of intermediate strings curr and booleanvisited matrices) but can that lead to TLE?

class Solution {
public:
    bool dfs(vector<vector<char>>& board, int m, int n, int i,  int j, string word, string curr, vector<vector<bool>> visited)
    {
        if (i<0 || i>=m || j<0 || j>=n || visited[i][j] || board[i][j]!=word[curr.length()]) return false;
        visited[i][j] = true;
        curr.push_back(board[i][j]);
        if (word==curr) return true;
        return dfs(board,m,n,i-1,j,word,curr,visited) ||
               dfs(board,m,n,i+1,j,word,curr,visited) ||
               dfs(board,m,n,i,j-1,word,curr,visited) ||
               dfs(board,m,n,i,j+1,word,curr,visited);
    }

	bool exist(vector<vector<char>>& board, string word) 
    {
        int m = board.size(), n = board[0].size();
        vector<vector<bool>> visited(m, vector<bool>(n,false));
        for (int i=0; i<m; i++)
        {
            for (int j=0; j<n; j++)
            {
                if (dfs(board, m, n, i, j, word, "", visited))
                    return true;
            }
        }
        return false;
    }
};

EDIT:

Based on other answers I modified above code to a low memory solution and it gets AC:

class Solution {
public:
    bool dfs(vector<vector<char>>& board, int m, int n, int i,  int j, string word, int index)
    {
        if (i<0 || i>=m || j<0 || j>=n || board[i][j]!=word[index]) return false;
        board[i][j] = '*';
        if (index==word.length()-1) return true;
        bool res =  dfs(board,m,n,i-1,j,word,index+1) ||
                       dfs(board,m,n,i+1,j,word,index+1) ||
                       dfs(board,m,n,i,j-1,word,index+1) ||
                       dfs(board,m,n,i,j+1,word,index+1);
        board[i][j] = word[index];
        return res;
    }
    bool exist(vector<vector<char>>& board, string word) 
    {
        int m = board.size(), n = board[0].size();
        for (int i=0; i<m; i++)
        {
            for (int j=0; j<n; j++)
            {
                if (dfs(board, m, n, i, j, word, 0))
                    return true;
            }
        }
        return false;
    }
};