Populating Next Right Pointers in Each Node II - Connections using Level Wise Traversal DFS

Binary Tree     Breadth-First Search     C++     Depth-First Search     Linked List     Medium     Tree    

Problem Statement:

Given a binary tree

struct Node {
  int val;
  Node *left;
  Node *right;
  Node *next;
}

Populate each next pointer to point to its next right node. If there is no next right node, the next pointer should be set to NULL.

Initially, all next pointers are set to NULL.

 

Example 1:

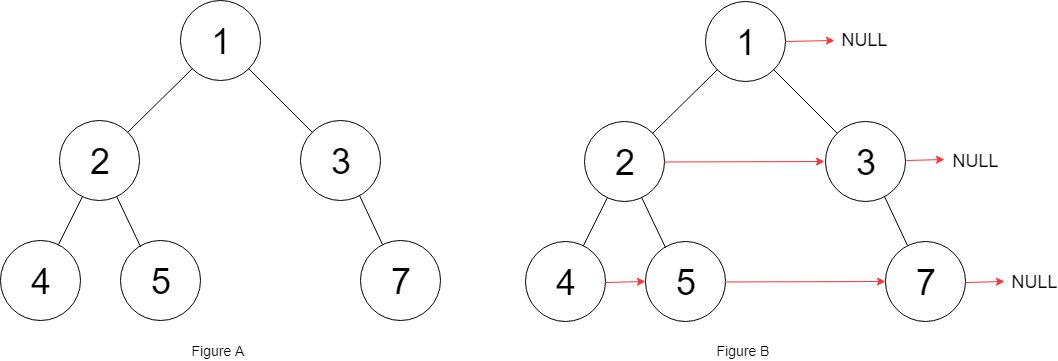
Input: root = [1,2,3,4,5,null,7]
Output: [1,#,2,3,#,4,5,7,#]
Explanation: Given the above binary tree (Figure A), your function should populate each next pointer to point to its next right node, just like in Figure B. The serialized output is in level order as connected by the next pointers, with '#' signifying the end of each level.

Example 2:

Input: root = []
Output: []

 

Constraints:

• The number of nodes in the tree is in the range [0, 6000].
• -100 <= Node.val <= 100

 

Follow-up:

• You may only use constant extra space.
• The recursive approach is fine. You may assume implicit stack space does not count as extra space for this problem.

Solution:

If you do not know level order traversal problem, refere here: Level Order Traversal - Two DFS solutions
Now we can immediately think of a solution: Instead of storing the keys, sotre the node pointers and then make required connections.

 
class Solution {
public:
    void dfs(Node *root, vector<vector<Node *>> &lvn, int level)
    {
        if (!root) return;
        if (level==lvn.size()) lvn.push_back({});
        lvn[level].push_back(root);
        dfs(root->left, lvn, level+1);
        dfs(root->right, lvn, level+1);
    }
    Node* connect(Node* root) {
        vector<vector<Node *>> levelWiseNodes;
        dfs(root, levelWiseNodes, 0);
        for (int i=0; i<levelWiseNodes.size(); i++)
        {
            if (levelWiseNodes[i].size()<2) continue;
            for (int j=0; j<=levelWiseNodes[i].size()-2; j++)
            {
               levelWiseNodes[i][j]->next = levelWiseNodes[i][j+1];
            }
        }
        return root;
    }
};