Minimum Falling Path Sum - DP Solution very straightforward | Seam Carving
Problem Statement:
Given an n x n array of integers matrix, return the minimum sum of any falling path through matrix.
A falling path starts at any element in the first row and chooses the element in the next row that is either directly below or diagonally left/right. Specifically, the next element from position (row, col) will be (row + 1, col - 1), (row + 1, col), or (row + 1, col + 1).
Example 1:
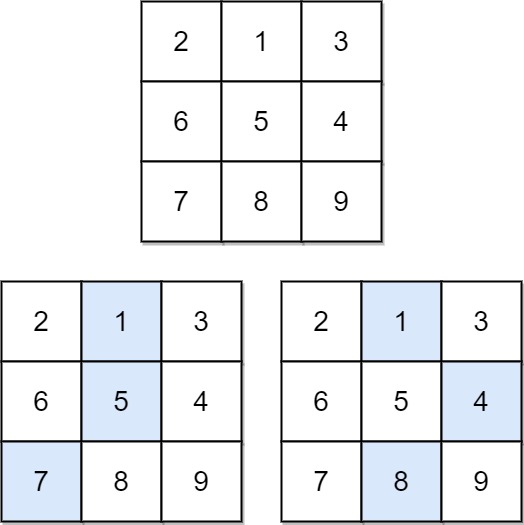
Input: matrix = [[2,1,3],[6,5,4],[7,8,9]] Output: 13 Explanation: There are two falling paths with a minimum sum as shown.
Example 2:
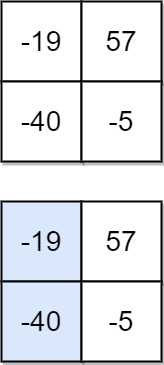
Input: matrix = [[-19,57],[-40,-5]] Output: -59 Explanation: The falling path with a minimum sum is shown.
Constraints:
n == matrix.length == matrix[i].length1 <= n <= 100-100 <= matrix[i][j] <= 100
Solution:
- Create a
dpmatrix of size (nxn) - Copy last row of
matrixto last row ofdp - Iteratively go up from
r=n-2tor=0. For element(r,c)the expression we have is:dp[r,c] = min(dp[r+1,c-1], dp[r+1,c], dp[r+1,c+1]) - For
c=0andc=n-1take min of only two elements rather than 3. These are left and right edges - After reaching top row, check which element in top row is the minimum.
- Done!
class Solution {
public:
int minFallingPathSum(vector<vector<int>>& matrix) {
int n = matrix.size();
vector<vector<int>> dp(n, vector<int>(n,0));
for (int c=0; c<n; c++) dp[n-1][c] = matrix[n-1][c];
for (int r=n-2; r>=0; r--)
{
for (int c=0; c<n; c++)
{
if (c==0) dp[r][c] = min(dp[r+1][c], dp[r+1][c+1]) + matrix[r][c];
else if (c==n-1) dp[r][c] = min(dp[r+1][c], dp[r+1][c-1]) + matrix[r][c];
else dp[r][c] = min(min(dp[r+1][c-1], dp[r+1][c]), dp[r+1][c+1]) + matrix[r][c];
}
}
int res=INT_MAX;
for (int c=0; c<n; c++) res = min(res, dp[0][c]);
return res;
}
};
BTW, this algorithm is used in a smart image resizing method known as Seam Carving.